
17.(本小题满分12分)
解:(Ⅰ)由题意可得,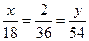 ,所以
,所以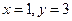 .
.
(Ⅱ)记从高校B抽取的2人为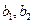 ,从高校C抽取的3人为
,从高校C抽取的3人为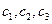 ,则从高校B,C抽取的5人中选2人作专题发言的基本事件有
,则从高校B,C抽取的5人中选2人作专题发言的基本事件有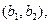
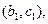
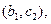
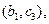
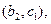
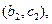
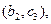
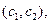
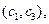
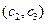 共10种.
共10种.
设选中的2人都来自高校C的事件为X,则X包含的基本事件有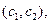
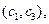
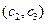 共3种.因此
共3种.因此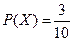 .
.
故选中的2人都来自高校C的概率为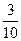 .
.
18.(本小题满分12分)
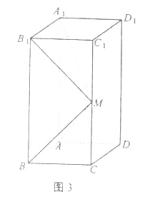
解:(Ⅰ)如图,因为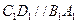 ,所以
,所以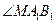 为异面直线
为异面直线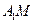 与
与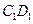 所成的角.
所成的角.
因为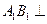 平面
平面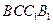 ,所以
,所以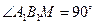 .
.
而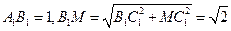 ,故
,故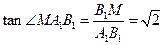 .
.
即异面直线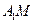 和
和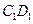 所成的角的正切值为
所成的角的正切值为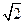 .
.
(Ⅱ)由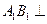 平面
平面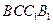 ,
,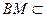 平面
平面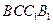 ,得
,得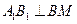 .①
.①
由(Ⅰ)知,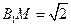 ,又
,又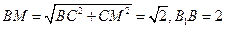 ,所以
,所以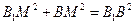 ,从而
,从而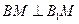 .②
.②
又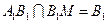 ,再由①,②得
,再由①,②得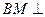 平面
平面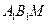 .而
.而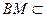 平面
平面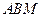 ,因此平面
,因此平面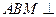 平面
平面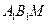 .
.
19.(本小题满分13分)
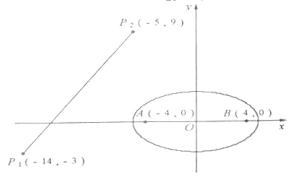
解:(Ⅰ)设边界曲线上点P的坐标为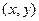 ,则由
,则由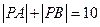 知,点P在以A,B为焦点,长轴长为
知,点P在以A,B为焦点,长轴长为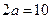 的椭圆上.此时短半轴长
的椭圆上.此时短半轴长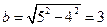 .
.
所以考察区域边界曲线(如图)的方程为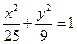 .
.
(Ⅱ)易知过点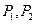 的直线方程为
的直线方程为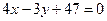 .因此点A到直线
.因此点A到直线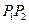 的距离为
的距离为

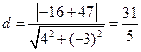 .
.
设经过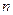 年,点A恰好在冰川边界线上,则利用等比数列求和公式可得
年,点A恰好在冰川边界线上,则利用等比数列求和公式可得
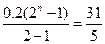 .
.
解得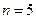 ,即经过5年,点A恰好在冰川边界线上.
,即经过5年,点A恰好在冰川边界线上.
20.(本小题满分13分)
解:(Ⅰ)表4为
1 3 5 7
4 8 12
12 20
32
它的第1,2,3,4行中的数的平均数分别是4,8,16,32,它们构成首项为4,公比为2的等比数列.
将这一结论推广到表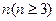 ,即表
,即表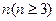 各行中的数的平均数按从上到下的顺序构成首项为
各行中的数的平均数按从上到下的顺序构成首项为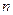 ,公比为2的等比数列.
,公比为2的等比数列.
简证如下(对考生不作要求)
首先,表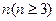 的第1行1,3,5,…,2n-1是等差数列,其平均数为
的第1行1,3,5,…,2n-1是等差数列,其平均数为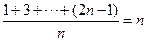 ;
;
其次,若表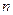 的第
的第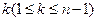 行
行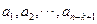 是等差数列,则它的第
是等差数列,则它的第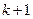 行
行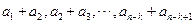 也是等差数列.由等差数列的性质知,表
也是等差数列.由等差数列的性质知,表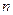 的第
的第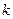 行中的数的平均数与第
行中的数的平均数与第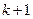 行中的数的平均数分别是
行中的数的平均数分别是
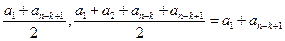 .
.

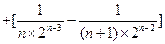
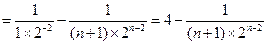
21.(本小题满分13分)
解:(Ⅰ)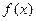 的定义域为
的定义域为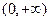 .
.
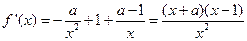 .
.
(1) 若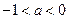 ,则当
,则当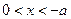 时,
时,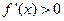 ;当
;当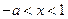 时,
时,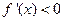 ;
;
当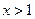 时,
时,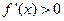 .故
.故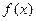 分别在
分别在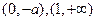 上单调递增,在
上单调递增,在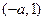 上单调递减.
上单调递减.
(2) 若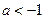 ,仿(1)可得
,仿(1)可得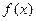 分别在
分别在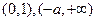 上单调递增,在
上单调递增,在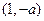 上单调递减.
上单调递减.
(Ⅱ)存在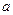 ,使
,使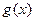 在
在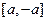 上为减函数.
上为减函数.
事实上,设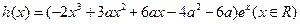 ,则
,则
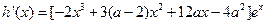 .
.
再设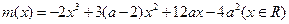 ,则当
,则当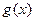 在
在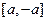 上单调递减时,
上单调递减时,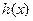 必在
必在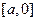 上单调递减,所以
上单调递减,所以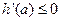 .由于
.由于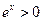 ,因此
,因此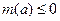 .而
.而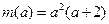 ,所以
,所以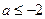 .此时,显然有
.此时,显然有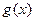 在
在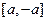 上为减函数,当且仅当
上为减函数,当且仅当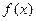 在
在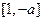 上为减函数,
上为减函数,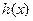 在
在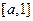 上为减函数,且
上为减函数,且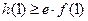 .
.
由(Ⅰ)知,当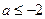 时,
时,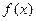 在
在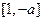 上为减函数.①
上为减函数.①
又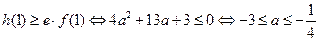 .②
.②
不难知道,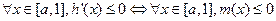 .
.
因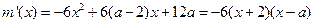 ,令
,令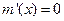 ,则
,则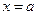 ,或
,或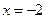 .而
.而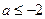 ,于是
,于是
(3) 当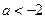 时,若
时,若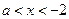 ,则
,则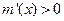 ;若
;若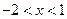 ,则
,则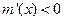 .因而
.因而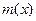 在
在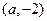 上单调递增,在
上单调递增,在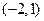 上单调递减.
上单调递减.
(4) 当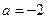 时,
时,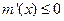 ,
,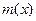 在
在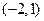 上单调递减.
上单调递减.
综合(1) 、(2)知,当
、(2)知,当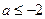 时,
时,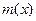 在
在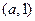 上的最大值为
上的最大值为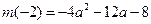 .
.
所以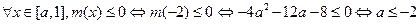 .③
.③
又对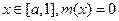 只有当
只有当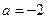 时在
时在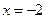 取得,亦即
取得,亦即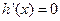 只有当
只有当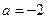 时在
时在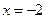 取得.因此,当
取得.因此,当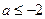 时,
时,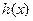 在
在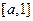 上为减函数.从而由①,②,③知,
上为减函数.从而由①,②,③知,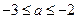 .
.
综上所述,存在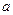 ,使
,使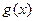 在
在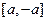 上为减函数,且
上为减函数,且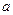 的取值范围为
的取值范围为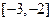 .
.











