一.选择题: 在每小题给出的四个选项中,只有一项是符合题目要求的.
(1) 已知集合A = {x∈R| |x|≤2}, B= {x∈R| x≤1}, 则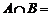
(A) 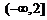 (B) [1,2](C) [-2,2](D) [-2,1]
(B) [1,2](C) [-2,2](D) [-2,1]
【答案】D
【解析】因为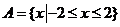 ,所以
,所以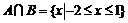 ,选D.
,选D.
(2) 设变量x, y满足约束条件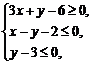 则目标函数
则目标函数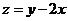 的最小值为
的最小值为
(A) -7(B) -4
(C) 1(D) 2
【答案】A
【解析】由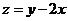 得
得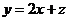 。作出可行域如图
。作出可行域如图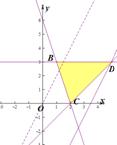 ,平移直线
,平移直线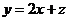 ,由图象可知当直线
,由图象可知当直线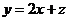 经过点D时,直线
经过点D时,直线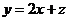 的截距最小,此时
的截距最小,此时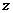 最小,由
最小,由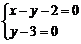 ,得
,得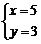 ,即
,即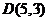 代入
代入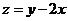 得
得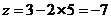 ,选A.
,选A.
(3) 阅读右边的程序框图, 运行相应的程序, 则输出n的值为
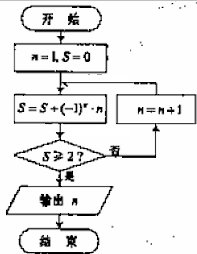
(A) 7(B) 6
(C) 5(D) 4
【答案】D
【解析】第一次循环,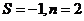 ;第二次循环,
;第二次循环,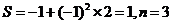 ;第三次循环,
;第三次循环,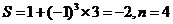 ;第四次循环,
;第四次循环,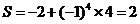 ,满足条件输出
,满足条件输出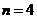 ,选D.
,选D.
(4) 设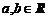 , 则 “
, 则 “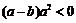 ”是“
”是“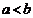 ”的
”的
(A) 充分而不必要条件
(B) 必要而不充分条件
(C) 充要条件
(D) 既不充分也不必要条件
【答案】A
【解析】若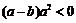 ,则
,则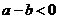 ,即
,即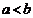 。若
。若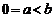 时
时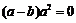 ,所以
,所以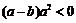 是
是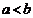 的充分而不必要条件,选A.
的充分而不必要条件,选A.
(5) 已知过点P(2,2) 的直线与圆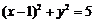 相切, 且与直线
相切, 且与直线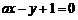 垂直, 则
垂直, 则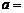
(A) 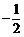 (B) 1
(B) 1
(C) 2(D) 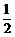
【答案】C
【解析】设直线斜率为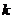 ,则直线方程为
,则直线方程为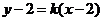 ,即
,即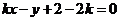 ,圆心
,圆心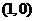 到直线的距离
到直线的距离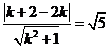 ,即
,即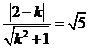 ,解得
,解得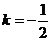 。因为直线与直线
。因为直线与直线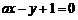 垂直,所以
垂直,所以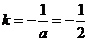 , 即
, 即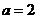 ,选C.
,选C.
(6) 函数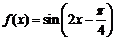 在区间
在区间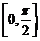 上的最小值是
上的最小值是
(A) 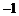 (B)
(B) 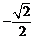
(C) 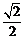 (D) 0
(D) 0
【答案】B
【解析】当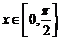 时,
时,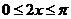 ,
,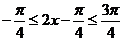 ,所以当
,所以当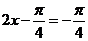 时,函数
时,函数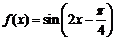 的最小值为
的最小值为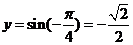 ,选B.
,选B.
(7) 已知函数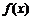 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间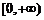 单调递增. 若实数a满足
单调递增. 若实数a满足 , 则a的取值范围是
, 则a的取值范围是
(A) 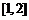 (B)
(B) 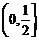
(C) 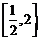 (D)
(D) 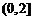
【答案】C
【解析】因为函数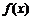 是定义在R上的偶函数,且
是定义在R上的偶函数,且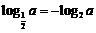 ,所以
,所以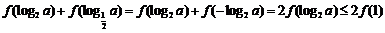 ,即
,即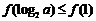 ,因为函数在区间
,因为函数在区间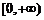 单调递增,所以
单调递增,所以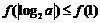 ,即
,即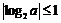 ,所以
,所以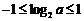 ,解得
,解得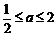 ,即a的取值范围是
,即a的取值范围是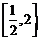 ,选C.
,选C.
(8) 设函数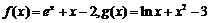 . 若实数a, b满足
. 若实数a, b满足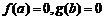 , 则
, 则
(A) 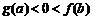 (B)
(B) 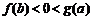
(C) 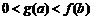 (D)
(D) 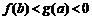
【答案】A
【解析】由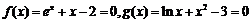 得
得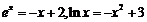 ,分别令
,分别令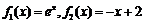 ,
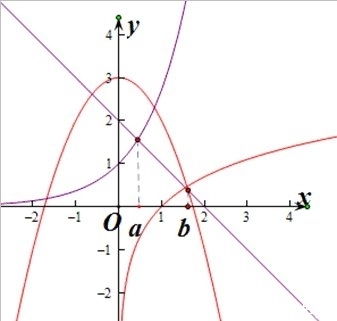
,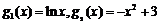 。在坐标系中分别作出函数
。在坐标系中分别作出函数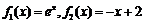 ,
,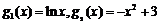 的图象,由图象知
的图象,由图象知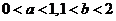 。此时
。此时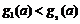 ,所以
,所以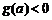 又。
又。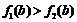 ,所以
,所以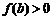 ,即
,即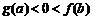 ,选A.
,选A.