第Ⅰ卷(共60分)
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只有一项是满足题目要求的.
1.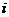 是虚数单位,复数
是虚数单位,复数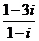 =
=
A.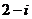 B.
B. 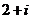 C.
C.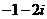 D.
D. 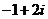
【答案】A
【解析】因为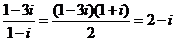 ,故选A.
,故选A.
2.设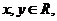 则“
则“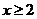 且
且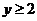 ”是“
”是“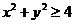 ”的
”的
A. 充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.即不充分也不必要条件
【答案】A
【解析】由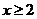 且
且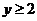 可得
可得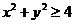 ,但反之不成立,故选A.
,但反之不成立,故选A.
3.阅读右边的程序框图,运行相应的程序,则输出 的值为
的值为
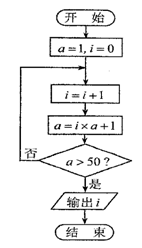
A.3 B.4 C.5 D.6
【答案】B
【解析】由程序框图知,选项B正确.
4.已知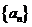 为等差数列,其公差为-2,且
为等差数列,其公差为-2,且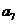 是
是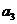 与
与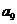 的等比中项,
的等比中项,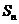 为
为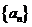 的前n项和,
的前n项和, 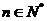 ,
,
则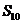 的值为
的值为

【解析】因为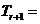
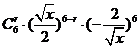 ,所以容易得C正确.
,所以容易得C正确.
6.如图,在△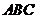 中,
中,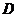 是边
是边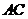 上的点,且
上的点,且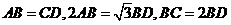 ,则
,则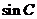 的值为( )
的值为( )
A.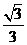 B.
B.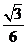
 C.
C.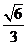 D.
D.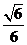
【答案】D
【解析】由正弦定理得D正确.
7.已知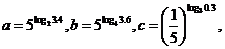 则( )
则( )
A.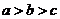 B.
B.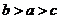 C.
C.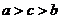 D.
D.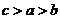
【答案】C
【解析】容易得选项D正确.
8.对实数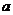 与
与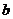 ,定义新运算“
,定义新运算“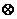 ”:
”: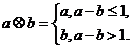 设函数
设函数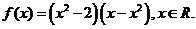 若函数
若函数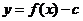 的图像与
的图像与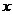 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数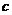 的取值范围是( )
的取值范围是( )
A.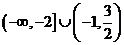 B.
B.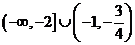
C.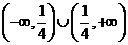
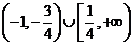 D.
D.
【答案】B
 CE与圆相切,则线段CE的长为 .
CE与圆相切,则线段CE的长为 .
【答案】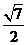
【解析】设AF=4x,BF==2x,BE=x,则由相交弦定理得: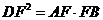 ,即
,即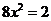 ,即
,即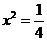 ,由切割线定理得:
,由切割线定理得: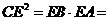
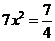 ,所以
,所以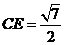 .
.
13.已知集合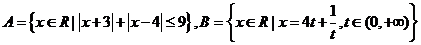 ,则集合
,则集合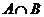 =________
=________
【答案】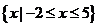
【解析】本小题考查集合的相关知识,属基础题.
14.已知直角梯形ABCD中,AD∥BC,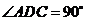 ,AD=2,BC=1,P是腰DC上的动点,则
,AD=2,BC=1,P是腰DC上的动点,则
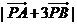 的最小值为 .
的最小值为 .
【答案】5
【解析】画出图形,容易得结果为5.
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数 ,
,
(Ⅰ)求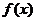 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设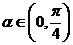 ,若
,若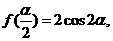 求
求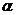 的大小.
的大小.
【答案】(Ⅰ)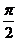 ;(Ⅱ)
;(Ⅱ)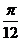

17.(本小题满分13分)
如图,在三棱柱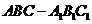 中,
中,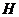 是正方形
是正方形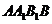 的中心,
的中心,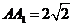 ,
,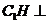 平面
平面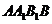 ,且
,且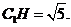
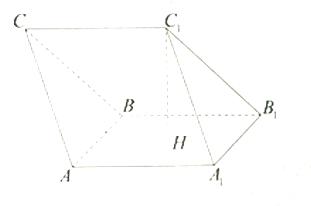
(Ⅰ)求异面直线与所成角的余弦值;
(Ⅱ )求二面角
)求二面角 的正弦值;
的正弦值;
(Ⅲ)设 为棱
为棱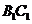 的中点,点
的中点,点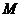 在平面
在平面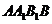 内,且
内,且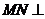 平面
平面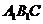 ,求线段
,求线段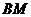 的长.
的长.
【答案】(Ⅰ)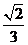 ;(Ⅱ)
;(Ⅱ)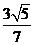 ;(Ⅲ)
;(Ⅲ)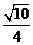
【过程详解请参见图片版】
【解析】参考标准答案.本小题主要考查直线与平面平行、直线与平面垂直、直线与平面所成的角等基础知识,考查空间想象能力、运算能力和推理论证能力.
18.(本小题满分13分)
在平面直角坐标系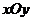 中,点
中,点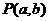
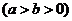 为动点,
为动点,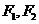 分别为椭圆
分别为椭圆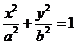 的左右焦点.已知△
的左右焦点.已知△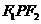 为等腰三角形.
为等腰三角形.
(Ⅰ)求椭圆的离心率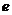 ;
;
(Ⅱ)设直线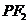 与椭圆相交于
与椭圆相交于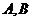 两点,
两点,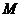 是直线
是直线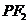 上的点,满足
上的点,满足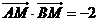 ,求点
,求点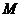 的轨迹方程.
的轨迹方程.
【答案】(Ⅰ)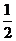 ;(Ⅱ)
;(Ⅱ)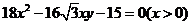

20.(本小题满分14分)
已知数列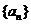 与
与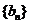 满足:
满足:
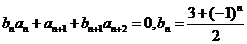 ,
, 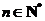 ,且
,且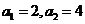 .
.
(Ⅰ)求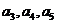 的值;
的值;
(Ⅱ)设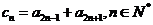 ,证明:
,证明: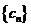 是等比数列;
是等比数列;
(Ⅲ)设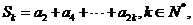 证明:
证明: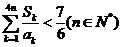 .
.
【答案】(Ⅰ)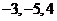
【过程详解请参见图片版】
【解析】参考标准答案.本小题主要等比数列的定义、数列求和等基础知识,考查运算能力、推理论证能力、综合分析能力和解决问题的能力及分类讨论的思想方法.











