(18)(本小题满分12分)
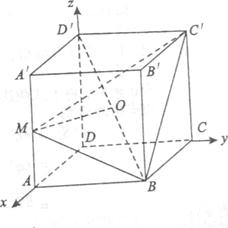
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
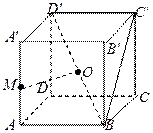
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
【命题意图】本题以正方体为载体,考查空间垂直关系的证明以及二面角的计算,考查基本的空间推理与计算能力,考查利用向量解决立体几何的能力.
解法一
(Ⅰ)连结AC,取AC的中点K,则K为BD的中点,连结OK.
因为点M是棱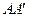 ′的中点,点O是
′的中点,点O是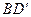 的中点,
的中点,
所以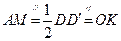 ,
,
所以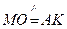 .
.
由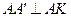 ,得
,得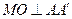
因为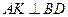 ,
,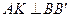 ,所以
,所以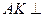 平面
平面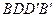 ,
,
所以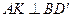 .
.
所以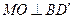 .
.
又因为OM与异面直线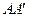 和
和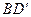 都相交,
都相交,
故OM为异面直线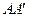 和
和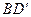 ’的公垂线.……………(5分)
’的公垂线.……………(5分)
(Ⅱ)取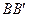 的中点N,连结MN,则
的中点N,连结MN,则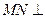 平面
平面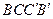 .过点N作
.过点N作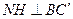 于H,连结MH,则由三垂线定理得,
于H,连结MH,则由三垂线定理得,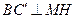 .从而,
.从而,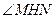 为二面角
为二面角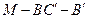 的平面角.
的平面角.
设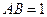 ,则
,则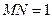 ,
,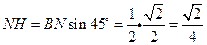 .
.
在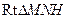 中,
中,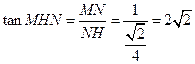 .
.
故二面角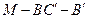 的大小为
的大小为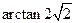 .……………………………(12分)
.……………………………(12分)
解法二
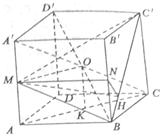
以点D为坐标原点,建立如图所示的空间直角坐标系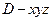 .设
.设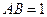 ,则
,则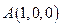 ,
,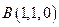 ,
,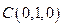 ,
,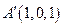 ,
,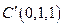 ,
,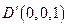 .
.

(Ⅱ)设平面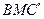 的一个法向量为
的一个法向量为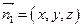 .
.
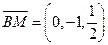 ,
,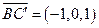 .
.
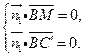 即
即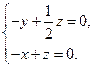
取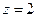 ,则
,则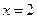 ,
,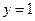 .从而
.从而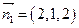 .
.
取平面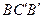 的一个法向量为
的一个法向量为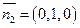 .
.
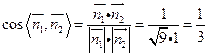 .
.
由图可知,二面角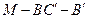 的平面角为锐角,
的平面角为锐角,
故二面角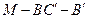 的大小为
的大小为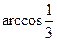 .……………………………(12分)
.……………………………(12分)
【点评】空间的线线垂直的证明方法主要有:(1)定义法;(2)等腰三角形的性质;(3)三垂线定理;(4)线面垂直;(5)向量法.几何法确定二面角的平面角的方法:(1)直接法;(2)三垂线法;(3)棱的垂面法等,当然如果题目适合建立空间直角坐标系,用向量法更简洁,但对于分步给分的立体几何解答题,传统法也有它的长处.
(19)(本小题满分12分)
(Ⅰ)1证明两角和的余弦公式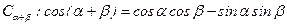 ;
;
2由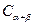 推导两角和的正弦公式
推导两角和的正弦公式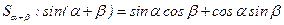 .
.
(Ⅱ)已知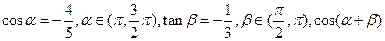 ,求
,求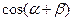
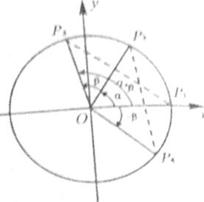
【命题意图】本题主要考查两角和的正、余弦公式、诱导公式、同角三角函数的关系等基础知识及运算能力.
解:(Ⅰ)①如图,在直角坐标系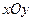 内作单位圆O,并作出角
内作单位圆O,并作出角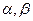 与
与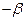 ,使角
,使角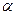 的始边为
的始边为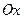 ,交
,交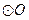 于点
于点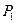 ,终边交
,终边交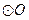 于点
于点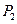 ;角
;角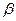 的始边为
的始边为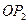 ,终边交
,终边交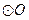 于点
于点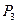 ,角
,角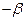 的始边为
的始边为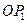 ,终边交
,终边交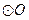 于点
于点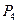 .
.
则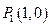 ,
,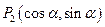 ,
,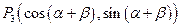 ,
,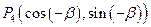 .
.
由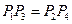 及两点间的距离公式,得
及两点间的距离公式,得
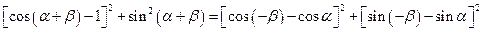
展开并整理,得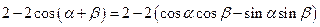 .
.
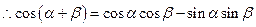 .……………(4分)
.……………(4分)
②由①易得,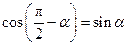 ,
,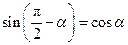 .
.
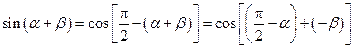
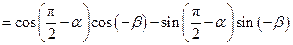
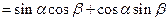 .
.
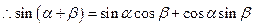 .……………………………(6分)
.……………………………(6分)
(Ⅱ)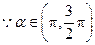 ,
,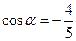 .
.
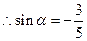 .
.
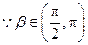 ,
,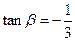 .
.
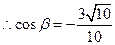 ,
,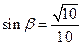 .
.
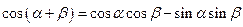
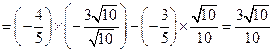 .………………………(12分)
.………………………(12分)












