一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应位置上。
1、已知集合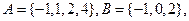 则
则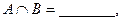
答案: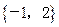
2、函数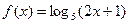 的单调增区间是__________
的单调增区间是__________
答案: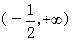
3、设复数i满足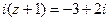 (i是虚数单位),则
(i是虚数单位),则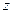 的实部是_________
的实部是_________
答案:1
4、根据如图所示的伪代码,当输入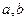 分别为2,3时,最后输出的m的值是________
分别为2,3时,最后输出的m的值是________
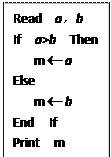
答案:3
5、从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是______
答案: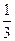
6、某老师从星期一到星期五收到信件数分别是10,6,8,5,6,则该组数据的方差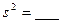
解析:可以先把这组数都减去6再求方差,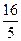
7、已知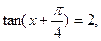 则
则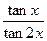 的值为__________
的值为__________
解析: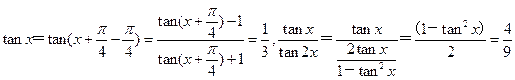
8、在平面直角坐标系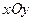 中,过坐标原点的一条直线与函数
中,过坐标原点的一条直线与函数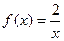 的图象交于P、Q两点,则线段PQ长的最小值是________
的图象交于P、Q两点,则线段PQ长的最小值是________
解析:4,设交点为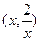 ,
,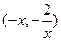 ,则
,则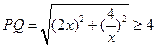
9、函数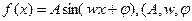 是常数,
是常数,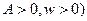 的部分图象如图所示,则
的部分图象如图所示,则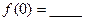
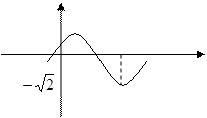
解析:由图可知: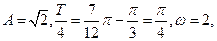
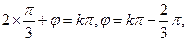
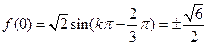
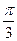
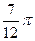
10、已知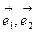 是夹角为
是夹角为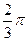 的两个单位向量,
的两个单位向量,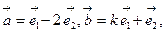 若
若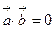 ,则k的值为
,则k的值为
解析:由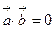 得:k=2
得:k=2
11、已知实数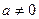 ,函数
,函数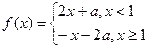 ,若
,若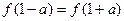 ,则a的值为________
,则a的值为________
解析: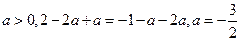 ,
,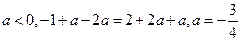
12、在平面直角坐标系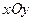 中,已知点P是函数
中,已知点P是函数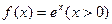 的图象上的动点,该图象在P处的切线
的图象上的动点,该图象在P处的切线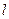 交y轴于点M,过点P作
交y轴于点M,过点P作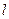 的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________
的垂线交y轴于点N,设线段MN的中点的纵坐标为t,则t的最大值是_____________
解析:设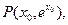 则
则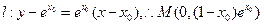 ,过点P作
,过点P作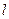 的垂线
的垂线
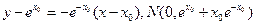 ,
,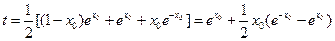
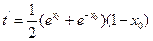 ,所以,t在
,所以,t在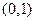 上单调增,在
上单调增,在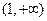 单调减,
单调减,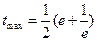 。
。
13、设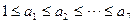 ,其中
,其中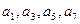 成公比为q的等比数列,
成公比为q的等比数列,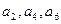 成公差为1的等差数列,则q的最小值是________
成公差为1的等差数列,则q的最小值是________
解析:由题意: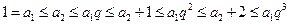 ,
,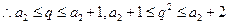
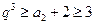 ,而
,而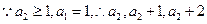 的最小值分别为1,2,3;
的最小值分别为1,2,3;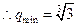 。
。
14、设集合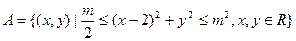 ,
, 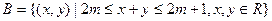 ,
,
若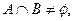 则实数m的取值范围是______________
则实数m的取值范围是______________
解析:当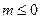 时,集合A是以(2,0)为圆心,以
时,集合A是以(2,0)为圆心,以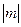 为半径的圆,集合B是在两条平行线之间,
为半径的圆,集合B是在两条平行线之间,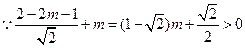 ,因为
,因为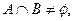 此时无解;当
此时无解;当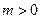 时,集合A是以(2,0)为圆心,以
时,集合A是以(2,0)为圆心,以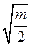 和
和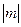 为半径的圆环,集合B是在两条平行线之间,必有
为半径的圆环,集合B是在两条平行线之间,必有 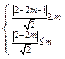
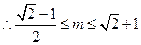 .又因为
.又因为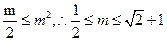
二、解答题:本大题共6小题,共90分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
15、(本小题满分14分)在△ABC中,角A、B、C所对应的边为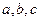
(1)若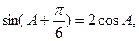 求A的值;
求A的值;
(2)若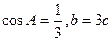 ,求
,求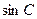 的值.
的值.
解析:(1)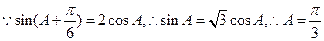
(2)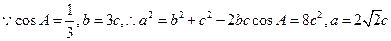
由正弦定理得: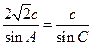 ,而
,而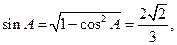
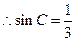 。(也可以先推出直角三角形)
。(也可以先推出直角三角形)
16、(本小题满分14分)如图,在四棱锥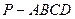 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
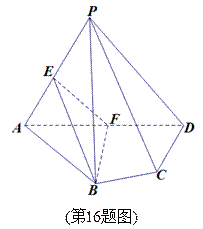
求证:(1)直线EF‖平面PCD;
(2)平面BEF⊥平面PAD
解析:(1)因为E、F分别是AP、AD的中点,
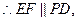 又
又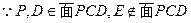
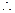 直线EF‖平面PCD
直线EF‖平面PCD
(2)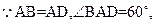 F是AD的中点,
F是AD的中点,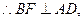
又平面PAD⊥平面ABCD,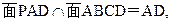
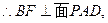
所以,平面BEF⊥平面PAD。
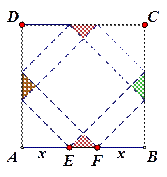
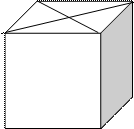
17、请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得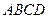 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
(1)若广告商要求包装盒侧面积S(cm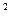 )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm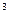 )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
P
解析:(1)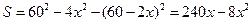 (0<x<30),所以x=15cm时侧面积最大,
(0<x<30),所以x=15cm时侧面积最大,
(2)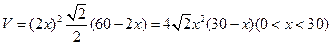 ,所以,
,所以,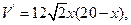
当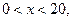 时,
时,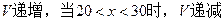 ,所以,当x=20时,V最大。
,所以,当x=20时,V最大。
此时,包装盒的高与底面边长的比值为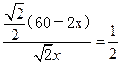
18、(本小题满分16分)如图,在平面直角坐标系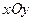 中,M、N分别是椭圆
中,M、N分别是椭圆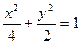 的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
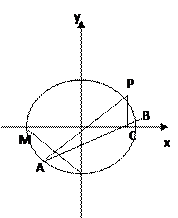
(1)当直线PA平分线段MN时,求k的值;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB
解析:(1)M(-2,0),N(0,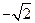 ),M、N的中点坐标为(-1,
),M、N的中点坐标为(-1,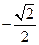 ),所以
),所以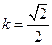
(2)由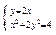 得
得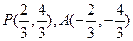 ,
,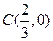 ,AC方程:
,AC方程: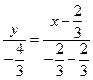 即:
即: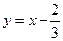
所以点P到直线AB的距离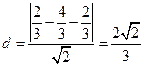
(3)法一:由题意设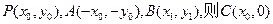 ,
,
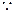 A、C、B三点共线,
A、C、B三点共线,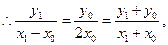 又因为点P、B在椭圆上,
又因为点P、B在椭圆上,
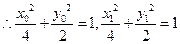 ,两式相减得:
,两式相减得: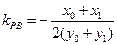
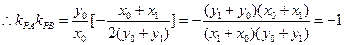
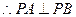
法二:设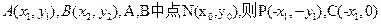 ,
,
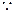 A、C、B三点共线,
A、C、B三点共线,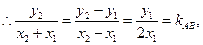 又因为点A、B在椭圆上,
又因为点A、B在椭圆上,
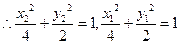 ,两式相减得:
,两式相减得: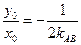 ,
,
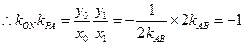 ,
,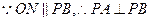
19、(本小题满分16分)已知a,b是实数,函数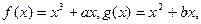
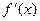 和
和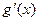 是
是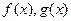 的导函数,若
的导函数,若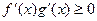 在区间I上恒成立,则称
在区间I上恒成立,则称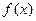 和
和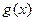 在区间I上单调性一致
在区间I上单调性一致
(1)设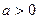 ,若函数
,若函数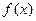 和
和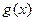 在区间
在区间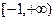 上单调性一致,求实数b的取值范围;
上单调性一致,求实数b的取值范围;
(2)设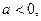 且
且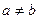 ,若函数
,若函数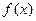 和
和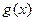 在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
在以a,b为端点的开区间上单调性一致,求|a-b|的最大值。
解析:(1)因为函数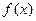 和
和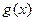 在区间
在区间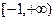 上单调性一致,所以,
上单调性一致,所以,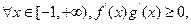 即
即
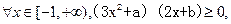
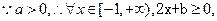
即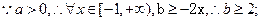
(2)当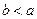 时,因为,函数
时,因为,函数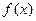 和
和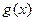 在区间(b,a)上单调性一致,所以,
在区间(b,a)上单调性一致,所以,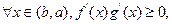
即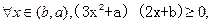
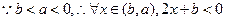 ,
,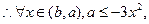
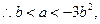 设
设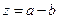 ,考虑点(b,a)的可行域,函数
,考虑点(b,a)的可行域,函数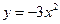 的斜率为1的切线的切点设为
的斜率为1的切线的切点设为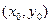
则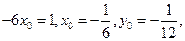
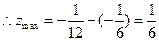 ;
;
当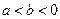 时,因为,函数
时,因为,函数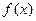 和
和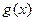 在区间(a, b)上单调性一致,所以,
在区间(a, b)上单调性一致,所以,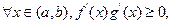
即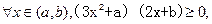
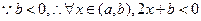 ,
,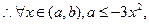
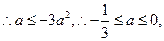
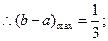
当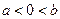 时,因为,函数
时,因为,函数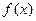 和
和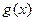 在区间(a, b)上单调性一致,所以,
在区间(a, b)上单调性一致,所以,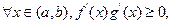
即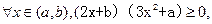
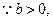 而x=0时,
而x=0时,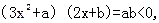 不符合题意,
不符合题意,
当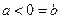 时,由题意:
时,由题意: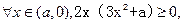
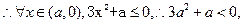
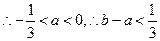
综上可知,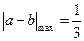 。
。











