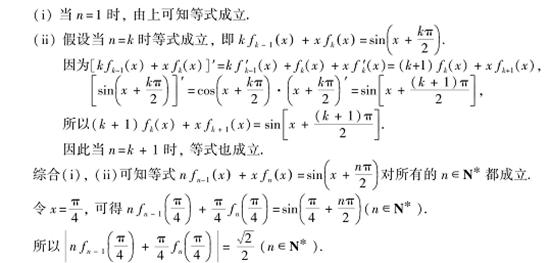一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1. 已知集合A={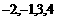 },
},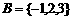 ,则
,则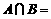 ______.
______.
2. 已知复数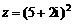 (i为虚数单位),则
(i为虚数单位),则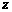 的实部为______.
的实部为______.
3. 右图是一个算法流程图,则输出的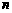 的值是______.
的值是______.

4. 从1,2,3,6这4个数中一次随机地取2个数,则所取2个数的乘积为6的概率是______.
5. 已知函数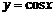 与
与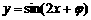 (0≤
(0≤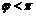 ),它们的图象有一个横坐标为
),它们的图象有一个横坐标为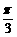 的交点,则
的交点,则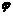 的值是______.
的值是______.
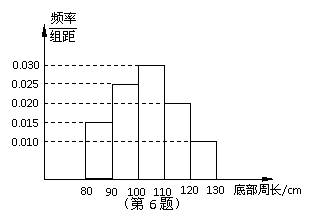
6. 设抽测的树木的底部周长均在区间[80,130]上,其频率分布直方图如图所示,则在抽测的60株树木中,有______株树木的底部周长小于100cm.
7. 在各项均为正数的等比数列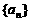 中,
中,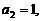
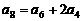 ,则
,则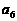 的值是______.
的值是______.
8. 设甲、乙两个圆柱的底面分别为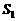 ,
,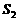 ,体积分别为
,体积分别为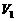 ,
,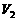 ,若它们的侧面积相等,且
,若它们的侧面积相等,且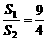 ,则
,则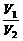 的值是______.
的值是______.
9. 在平面直角坐标系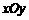 中,直线
中,直线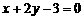 被圆
被圆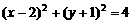 截得的弦长为______.
截得的弦长为______.
10. 已知函数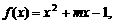 若对于任意
若对于任意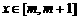 ,都有
,都有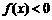 成立,则实数
成立,则实数 的取值范围是______.
的取值范围是______.
11. 在平面直角坐标系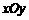 中,若曲线
中,若曲线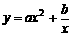 (a,b为常数)过点
(a,b为常数)过点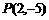 ,且该曲线在点P处的切线与直线
,且该曲线在点P处的切线与直线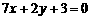 平行,则
平行,则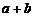 的值是______.
的值是______.
12. 如图,在平行四边形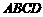 中,已知
中,已知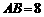 ,
,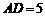 ,
,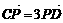 ,
,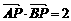 ,则
,则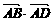 的值是______.
的值是______.

13. 已知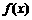 是定义在R上且周期为3的函数,当
是定义在R上且周期为3的函数,当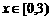 时,
时,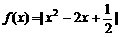 .若函数
.若函数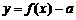 在区间
在区间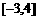 上有10个零点(互不相同),则实数
上有10个零点(互不相同),则实数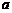 的取值范围是______.
的取值范围是______.
14. 若△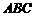 的内角满足
的内角满足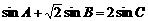 ,则
,则 的最小值是______.
的最小值是______.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
已知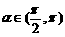 ,
,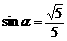 .
.
(1)求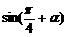 的值;
的值;
(2)求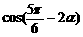 的值.
的值.
16.(本小题满分14分)
如图,在三棱锥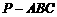 中,
中,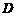 ,E,F分别为棱
,E,F分别为棱 的中点.已知
的中点.已知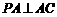 ,
,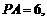
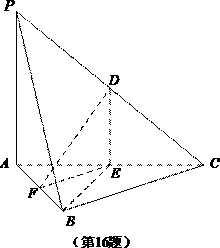
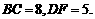
求证:
(1)直线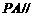 平面
平面 ;
;
(2)平面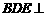 平面
平面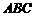 .
.
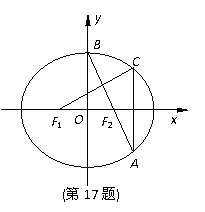
17.(本小题满分14分)
如图,在平面直角坐标系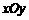 中,
中,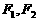 分别是椭圆
分别是椭圆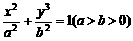 的左、右焦点,顶点
的左、右焦点,顶点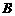 的坐标为
的坐标为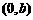 ,连结
,连结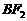 并延长交椭圆于点A,过点A作
并延长交椭圆于点A,过点A作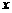 轴的垂线交椭圆于另一点C,连结
轴的垂线交椭圆于另一点C,连结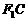 .
.
(1)若点C的坐标为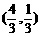 ,且
,且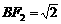 ,求椭圆的方程;
,求椭圆的方程;
(2)若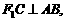 求椭圆离心率e的值.
求椭圆离心率e的值.
18.(本小题满分16分)
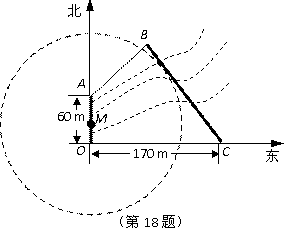
如图,为了保护河上古桥 ,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.且古桥两端O和A到该圆上任意一点的距离均不少于80m. 经测量,点A位于点O正北方向60m处, 点C位于点O正东方向170m处(OC为河岸),
,规划建一座新桥BC,同时设立一个圆形保护区.规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆.且古桥两端O和A到该圆上任意一点的距离均不少于80m. 经测量,点A位于点O正北方向60m处, 点C位于点O正东方向170m处(OC为河岸),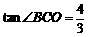 .
.
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
19.(本小题满分16分)
已知函数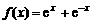 ,其中e是自然对数的底数.
,其中e是自然对数的底数.
(1)证明: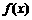 是R上的偶函数;
是R上的偶函数;
(2)若关于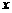 的不等式
的不等式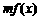 ≤
≤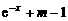 在
在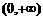 上恒成立,求实数
上恒成立,求实数 的取值范围;
的取值范围;
(3)已知正数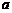 满足:存在
满足:存在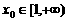 ,使得
,使得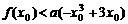 成立.试比较
成立.试比较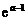 与
与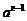 的大小,并证明你的结论.
的大小,并证明你的结论.
20.(本小题满分16分)
设数列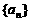 的前
的前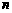 项和为
项和为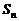 .若对任意正整数
.若对任意正整数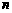 ,总存在正整数
,总存在正整数 ,使得
,使得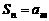 ,则称
,则称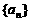 是“H数列”.
是“H数列”.
(1)若数列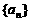 的前n项和
的前n项和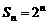 (
( N
N ),证明:
),证明: 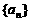 是“H数列”;
是“H数列”;
(2)设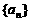 是等差数列,其首项
是等差数列,其首项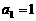 ,公差
,公差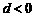 .若
.若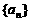 是“H数列”,求
是“H数列”,求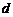 的值;
的值;
(3)证明:对任意的等差数列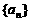 ,总存在两个“H数列”
,总存在两个“H数列”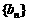 和
和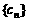 ,使得
,使得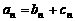 (
( N
N )成立.
)成立.
数学Ⅱ(附加题)
21.【选做题】本题包括A、B、C、D四小题,请选定其中两小题,并在相应的答题区域内作答.若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.
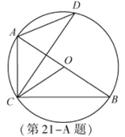 A.[选修4-1:几何证明选讲](本小题满分10分)
A.[选修4-1:几何证明选讲](本小题满分10分)
如图,AB是圆O的直径,C,D是圆O上位于AB异侧的两点.证明: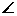 OCB=
OCB= 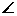 D.
D.
B.[选修4-2:矩阵与变换](本小题满分10分)
已知矩阵 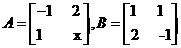 ,向量
,向量 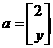 ,x,y为实数.
,x,y为实数.
若Aa =Ba,
求x+y的值.
C.[选修4-4:坐标系与参数方程](本小题满分10分)
在平面直角坐标系xOy中,已知直线 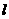 的参数方程为
的参数方程为 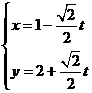 (t为参数),直线
(t为参数),直线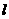 与抛物线
与抛物线 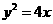 相交于A,B两点,求线段AB的长.
相交于A,B两点,求线段AB的长.
D.[选修4-5:不等式选讲](本小题满分10分)
已知x>0,y>0,证明: 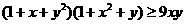 .
.
【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
22.(本小题满分10分)
盒中共有9个球,其中有4个红球、3个黄球和2个绿球,这些球除颜色外完全相同.
(l)从盒中一次随机取出2个球,求取出的2个球颜色相同的概率P;
(2)从盒中一次随机取出 4个球,其中红球、黄球、绿球的个数分别记为 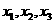 ,随机变量X表示
,随机变量X表示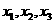 中的最大数,求X的概率分布和数学期望E(X).
中的最大数,求X的概率分布和数学期望E(X).
23.(本小题满分10分)
已知函数 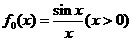 ,设
,设 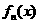 为
为 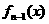 的导数,
的导数,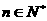 .
.
(1)求 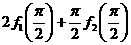 的值;
的值;
(2)证明:对任意的 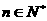 ,等式
,等式 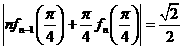 都成立.
都成立.