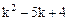一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.(2012年江苏省5分)已知集合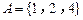 ,
,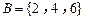 ,则
,则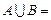 .
.
【答案】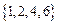 。
。
【考点】集合的概念和运算。
【分析】由集合的并集意义得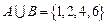 。
。
2.(2012年江苏省5分)某学校高一、高二、高三年级的学生人数之比为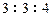 ,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 名学生.
,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 名学生.
【答案】15。
【考点】分层抽样。
【解析】分层抽样又称分类抽样或类型抽样。将总体划分为若干个同质层,再在各层内随机抽样或机械抽样,分层抽样的特点是将科学分组法与抽样法结合在一起,分组减小了各抽样层变异性的影响,抽样保证了所抽取的样本具有足够的代表性。因此,由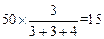 知应从高二年级抽取15名学生。
知应从高二年级抽取15名学生。
3.(2012年江苏省5分)设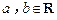 ,
,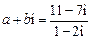 (i为虚数单位),则
(i为虚数单位),则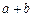 的值为 .
的值为 .
【答案】8。
【考点】复数的运算和复数的概念。
【分析】由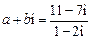 得
得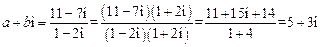 ,所以
,所以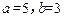 ,
,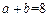 。
。
4.(2012年江苏省5分)下图是一个算法流程图,则输出的k的值是 .
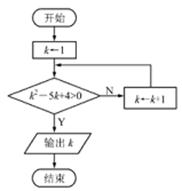
【答案】5。
【考点】程序框图。
【分析】根据流程图所示的顺序,程序的运行过程中变量值变化如下表:
是否继续循环 | k |
| |
循环前 | 0 | 0 | |
第一圈 | 是 | 1 | 0 |
第二圈 | 是 | 2 | -2 |
第三圈 | 是 | 3 | -2 |
第四圈 | 是 | 4 | 0 |
第五圈 | 是 | 5 | 4 |
第六圈 | 否 | 输出5 |
∴最终输出结果k=5。
5.(2012年江苏省5分)函数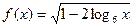 的定义域为 .
的定义域为 .
【答案】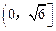 。
。
【考点】函数的定义域,二次根式和对数函数有意义的条件,解对数不等式。
【解析】根据二次根式和对数函数有意义的条件,得
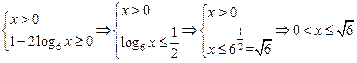 。
。
6.(2012年江苏省5分)现有10个数,它们能构成一个以1为首项,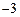 为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是 .
为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是 .
【答案】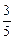 。
。
【考点】等比数列,概率。
【解析】∵以1为首项,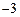 为公比的等比数列的10个数为1,-3,9,-27,···其中有5个负数,1个正数1计6个数小于8,
为公比的等比数列的10个数为1,-3,9,-27,···其中有5个负数,1个正数1计6个数小于8,
∴从这10个数中随机抽取一个数,它小于8的概率是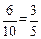 。
。
7.(2012年江苏省5分)如图,在长方体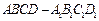 中,
中,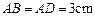 ,
,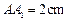 ,则四棱锥
,则四棱锥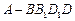 的体积为 cm3.
的体积为 cm3.
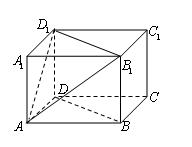
【答案】6。
【考点】正方形的性质,棱锥的体积。
【解析】∵长方体底面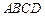 是正方形,∴△
是正方形,∴△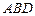 中
中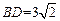 cm,
cm,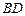 边上的高是
边上的高是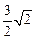 cm(它也是
cm(它也是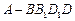 中
中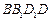 上的高)。
上的高)。
∴四棱锥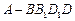 的体积为
的体积为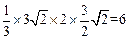 。由
。由
8.(2012年江苏省5分)在平面直角坐标系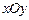 中,若双曲线
中,若双曲线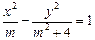 的离心率为
的离心率为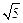 ,则
,则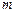 的值为 .
的值为 .
【答案】2。
【考点】双曲线的性质。
【解析】由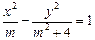 得
得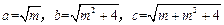 。
。
∴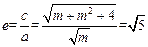 ,即
,即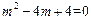 ,解得
,解得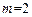 。
。
9.(2012年江苏省5分)如图,在矩形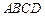 中,
中,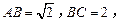 点
点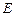 为
为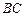 的中点,点
的中点,点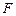 在边
在边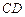 上,若
上,若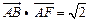 ,则
,则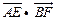 的值是 .
的值是 .
【答案】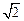 。
。
【考点】向量的计算,矩形的性质,三角形外角性质,和的余弦公式,锐角三角函数定义。
【解析】由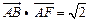 ,得
,得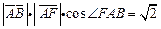 ,由矩形的性质,得
,由矩形的性质,得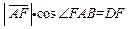 。
。
∵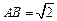 ,∴
,∴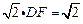 ,∴
,∴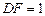 。∴
。∴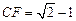 。
。
记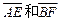 之间的夹角为
之间的夹角为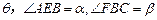 ,则
,则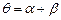 。
。
又∵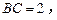 点E为BC的中点,∴
点E为BC的中点,∴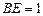 。
。
∴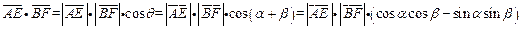
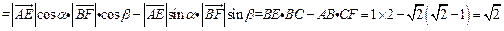 。
。
本题也可建立以 为坐标轴的直角坐标系,求出各点坐标后求解。
为坐标轴的直角坐标系,求出各点坐标后求解。
10.(2012年江苏省5分)设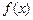 是定义在
是定义在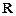 上且周期为2的函数,在区间
上且周期为2的函数,在区间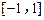 上,
上,
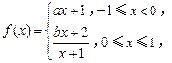 其中
其中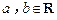 .若
.若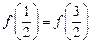 ,
,
则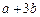 的值为 .
的值为 .
【答案】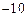 。
。
【考点】周期函数的性质。
【解析】∵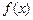 是定义在
是定义在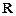 上且周期为2的函数,∴
上且周期为2的函数,∴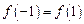 ,即
,即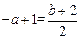 ①。
①。
又∵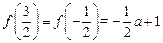 ,
,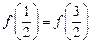 ,
,
∴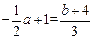 ②。
②。
联立①②,解得,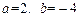 。∴
。∴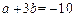 。
。
11.(2012年江苏省5分)设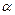 为锐角,若
为锐角,若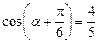 ,则
,则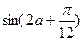 的值为 .
的值为 .
【答案】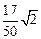 。
。
【考点】同角三角函数,倍角三角函数,和角三角函数。
【解析】∵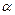 为锐角,即
为锐角,即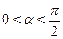 ,∴
,∴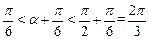 。
。
∵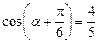 ,∴
,∴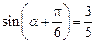 。∴
。∴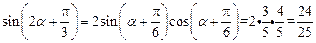 。
。
∴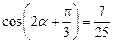 。
。
∴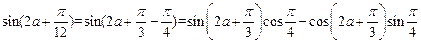
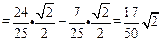 。
。
12.(2012年江苏省5分)在平面直角坐标系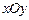 中,圆
中,圆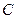 的方程为
的方程为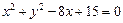 ,若直线
,若直线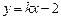
上至少存在一点,使得以该点为圆心,1为半径的圆与圆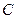 有公共点,则
有公共点,则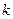 的最大值是 .
的最大值是 .
【答案】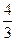 。
。
【考点】圆与圆的位置关系,点到直线的距离
【解析】∵圆C的方程可化为: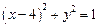 ,∴圆C的圆心为
,∴圆C的圆心为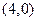 ,半径为1。
,半径为1。
∵由题意,直线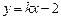 上至少存在一点
上至少存在一点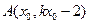 ,以该点为圆心,1为半径的圆与圆
,以该点为圆心,1为半径的圆与圆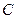 有
有
公共点;
∴存在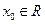 ,使得
,使得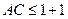 成立,即
成立,即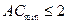 。
。
∵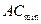 即为点
即为点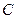 到直线
到直线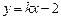 的距离
的距离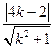 ,∴
,∴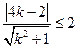 ,解得
,解得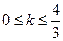 。
。
∴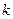 的最大值是
的最大值是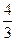 。
。
13.(2012年江苏省5分)已知函数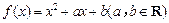 的值域为
的值域为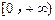 ,若关于x的不等式
,若关于x的不等式
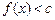 的解集为
的解集为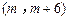 ,则实数c的值为 .
,则实数c的值为 .
【答案】9。
【考点】函数的值域,不等式的解集。
【解析】由值域为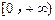 ,当
,当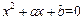 时有
时有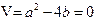 ,即
,即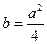 ,
,
∴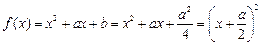 。
。
∴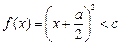 解得
解得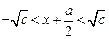 ,
,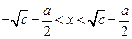 。
。
∵不等式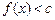 的解集为
的解集为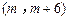 ,∴
,∴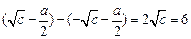 ,解得
,解得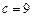 。
。
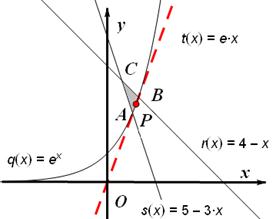
14.(2012年江苏省5分)已知正数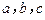 满足:
满足: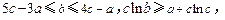 则
则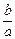 的取值范围是 .
的取值范围是 .
 【答案】
【答案】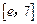 。
。
【考点】可行域。
【解析】条件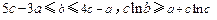 可化为:
可化为: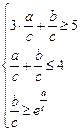 。
。
设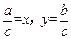 ,则题目转化为:
,则题目转化为:
已知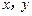 满足
满足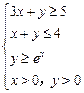 ,求
,求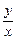 的取值范围。
的取值范围。
作出(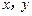 )所在平面区域(如图)。求出
)所在平面区域(如图)。求出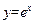 的切
的切
线的斜率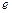 ,设过切点
,设过切点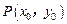 的切线为
的切线为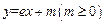 ,
,
则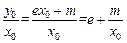 ,要使它最小,须
,要使它最小,须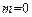 。
。
∴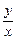 的最小值在
的最小值在 处,为
处,为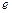 。此时,点
。此时,点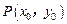 在
在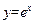 上
上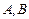 之间。
之间。
当(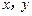 )对应点
)对应点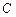 时,
时, 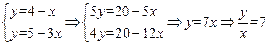 ,
,
∴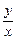 的最大值在
的最大值在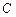 处,为7。
处,为7。
∴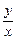 的取值范围为
的取值范围为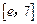 ,即
,即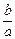 的取值范围是
的取值范围是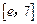 。
。