一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1.直线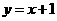 与圆
与圆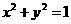 的位置关系为( )
的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
2.已知复数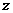 的实部为
的实部为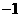 ,虚部为2,则
,虚部为2,则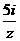 =( )
=( )
A.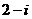 B.
B.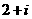 C.
C.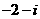 D.
D.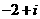
3.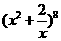 的展开式中
的展开式中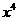 的系数是( )
的系数是( )
A.16 B.70 C.560 D.1120
4.已知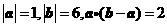 ,则向量
,则向量 与向量
与向量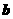 的夹角是( )
的夹角是( )
A.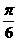 B.
B.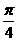 C.
C.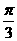 D.
D.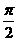

5.不等式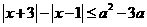 对任意实数
对任意实数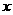 恒成立,则实数
恒成立,则实数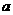 的取值范围为( )
的取值范围为( )
A. B.
B.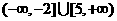 C.
C.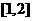 D.
D.
6.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为( )
A.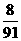 B.
B.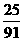 C.
C.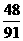 D.
D.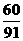
7.设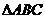 的三个内角
的三个内角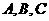 ,向量
,向量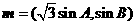 ,
,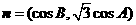 ,若
,若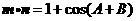 ,则
,则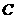 =( )
=( )
A.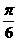 B.
B.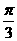 C.
C.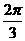 D.
D.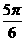
8.已知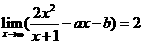 ,其中
,其中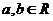 ,则
,则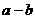 的值为( )
的值为( )
A.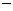 6 B.
6 B.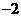 C.
C.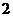 D.
D.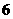
9.已知二面角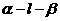 的大小为
的大小为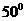 ,
,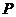 为空间中任意一点,则过点
为空间中任意一点,则过点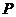 且与平面
且与平面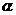 和平面
和平面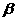 所成的角都是
所成的角都是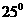 的直线的条数为( )
的直线的条数为( )
A.2 B.3 C.4 D.5
10.已知以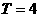 为周期的函数
为周期的函数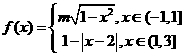 ,其中
,其中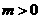 。若方程
。若方程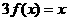 恰有5个实数解,则
恰有5个实数解,则 的取值范围为( )
的取值范围为( )
A.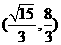 B.
B.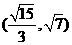 C.
C.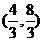 D.
D.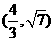
二、填空题:本大题共5小题,每小题5分,共25分.把答案写在答题卡相应位置上.
11.若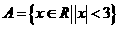 ,
,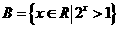 ,则
,则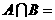 ___________.
___________.
12.若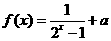 是奇函数,则
是奇函数,则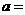 __________.
__________.
13.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有__________种(用数字作答).
14.设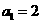 ,
,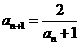 ,
,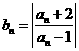 ,
,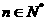 ,则数列
,则数列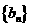 的通项公式
的通项公式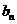 = __________.
= __________.
15.已知双曲线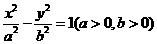 的左、右焦点分别为
的左、右焦点分别为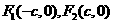 ,若双曲线上存在一点
,若双曲线上存在一点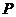 使
使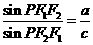 ,则该双曲线的离心率的取值范围是__________.
,则该双曲线的离心率的取值范围是__________.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数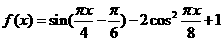 .
.
(Ⅰ)求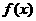 的最小正周期.
的最小正周期.
(Ⅱ)若函数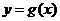 与
与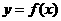 的图像关于直线
的图像关于直线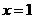 对称,求当
对称,求当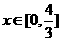 时
时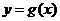 的最大值.
的最大值.
17.(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为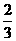 和
和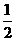 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数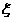 的分布列与期望.
的分布列与期望.
18.(本小题满分13分,(Ⅰ)问5分,(Ⅱ)问8分)
设函数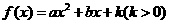 在
在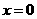 处取得极值,且曲线
处取得极值,且曲线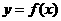 在点
在点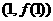 处的切线垂直于直线
处的切线垂直于直线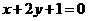 .
.
(Ⅰ)求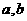 的值;
的值;
(Ⅱ)若函数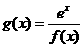 ,讨论
,讨论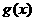 的单调性.
的单调性. 
19.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
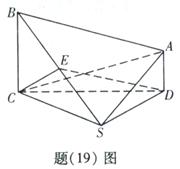
如题(19)图,在四棱锥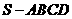 中,
中,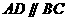 且
且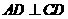 ;平面
;平面
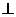 平面
平面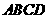 ,
,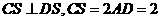 ;
;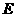 为
为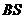 的中点,
的中点,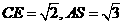 .求:
.求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角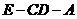 的大小.
的大小.
20.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为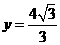 ,离心率
,离心率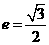 ,
, 是椭圆上的动点.
是椭圆上的动点.
(Ⅰ)若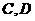 的坐标分别是
的坐标分别是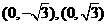 ,求
,求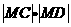 的最大值;
的最大值;
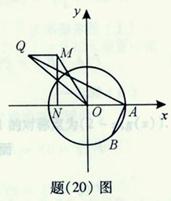
(Ⅱ)如题(20)图,点 的坐标为
的坐标为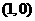 ,
,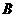 是圆
是圆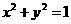 上的点,
上的点,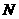 是点
是点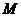 在
在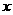 轴上的射影,点
轴上的射影,点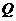 满足条件:
满足条件: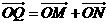 ,
,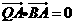 .求线段
.求线段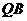 的中点
的中点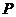 的轨迹方程;
的轨迹方程;
21.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设 个不全相等的正数
个不全相等的正数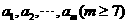 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)若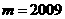 ,且
,且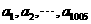 是公差为
是公差为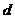 的等差数列,而
的等差数列,而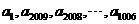 是公比为
是公比为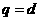 的等比数列;数列
的等比数列;数列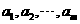 的前
的前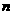 项和
项和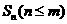 满足:
满足: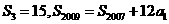 ,求通项
,求通项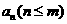 ;
;
(Ⅱ)若每个数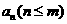 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证: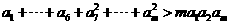 ;
;