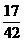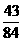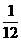一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在复平面内表示复数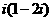 的点位于( )
的点位于( )
 第一象限
第一象限 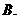 第二象限
第二象限
 第三象限
第三象限 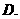 第四象限
第四象限
【答案】A
【解析】
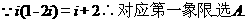
2.对任意等比数列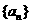 ,下列说法一定正确的是( )
,下列说法一定正确的是( )
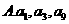 成等比数列
成等比数列 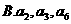 成等比数列
成等比数列
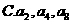 成等比数列
成等比数列 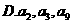 成等比数列
成等比数列
【答案】D
【解析】
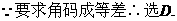
3.已知变量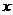 与
与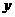 正相关,且由观测数据算得样本的平均数
正相关,且由观测数据算得样本的平均数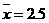 ,
,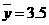 ,则由观测的数据得线性回归方程可能为( )
,则由观测的数据得线性回归方程可能为( )
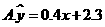
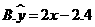
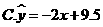
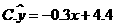
【答案】A
【解析】
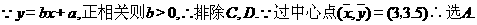
4.已知向量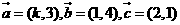 ,且
,且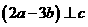 ,则实数k=
,则实数k=
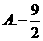
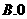 C.3 D.
C.3 D. 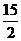
【答案】C
【解析】
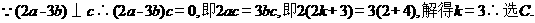
5.执行如题(5)图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是。
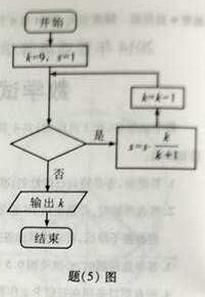
A.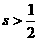 B.
B.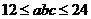
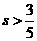 C.
C. 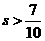 D.
D.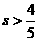
【答案】C
【解析】
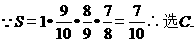
6.已知命题
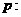 对任意
对任意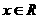 ,总有
,总有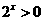 ;
;
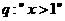 是
是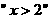 的充分不必要条件
的充分不必要条件
则下列命题为真命题的是( )
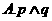
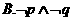
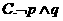
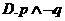
【答案】D
【解析】

7.某几何体的三视图如图所示,则该几何体的表面积为( )
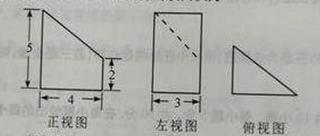
A.54 B.60 C.66 D.72
【答案】B
【解析】
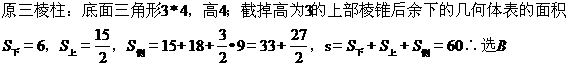
8.设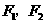 分别为双曲线
分别为双曲线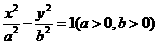 的左、右焦点,双曲线上存在一点
的左、右焦点,双曲线上存在一点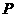 使得
使得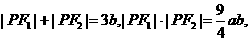 则该双曲线的离心率为( )
则该双曲线的离心率为( )
A.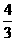 B.
B.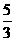 C.
C.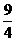 D.3
D.3
【答案】B
【解析】
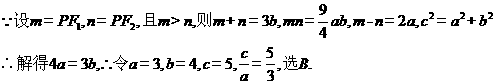
9.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则 类节目不相邻的排法种数是( )
A.72 B.120 C.144 D.3
【答案】B
【解析】解析完成时间2014-6-12qq373780592

10.已知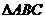 的内角
的内角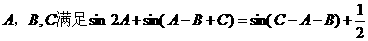 ,面积满足
,面积满足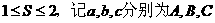 所对的边,则下列不等式成立的是( )
所对的边,则下列不等式成立的是( )
A.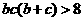 B.
B.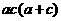 C.
C.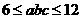 D.
D. 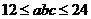
【答案】A
【解析】2014-6-12qq373780592

二、填空题 本大题共6小题,考生作答5小题,每小题5分,共25分,把答案填在答题卡相应位置上。
11.设全集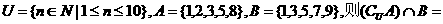 ______.
______.
【答案】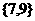
【解析】
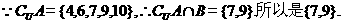
12.函数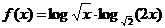 的最小值为_________.
的最小值为_________.
【答案】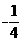
【解析】
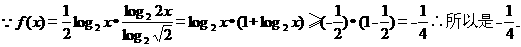
13. 已知直线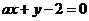 与圆心为
与圆心为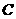 的圆
的圆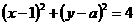 相交于
相交于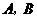 两点,且
两点,且
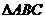 为等边三角形,则实数
为等边三角形,则实数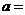 _________.
_________.
【答案】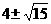
【解析】

考生注意:14、15、16三题为选做题,请从中任选两题作答,若三题全做,则按前两题给分.
14. 过圆外一点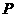 作圆的切线
作圆的切线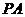 (
( 为切点),再作割线
为切点),再作割线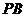 ,
,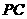 分别交圆于
分别交圆于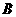 ,
,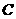 ,
,
若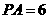 ,AC=8,BC=9,则AB=________.
,AC=8,BC=9,则AB=________.
【答案】4
【解析】
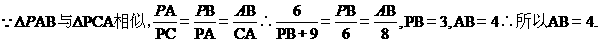
15. 已知直线 的参数方程为
的参数方程为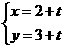 (
(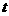 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,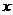 正半轴为极轴
正半轴为极轴
线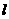 与曲线
与曲线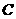 的公共点的极经
的公共点的极经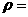 ________.
________.
【答案】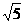
【解析】
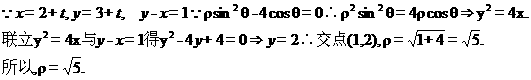
16. 若不等式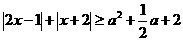 对任意实数
对任意实数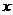 恒成立,则实数
恒成立,则实数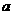 的取值范围是
的取值范围是
____________.
【答案】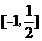
【解析】
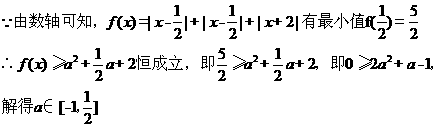
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算过程.
17. (本小题13分,(I)小问5分,(II)小问8分)
已知函数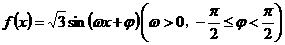 的图像关于直线
的图像关于直线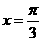 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为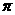 .
.
(I)求 和
和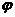 的值;
的值;
(II)若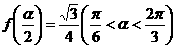 ,求
,求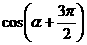 的值.
的值.
【答案】(I) 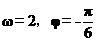 (II)
(II)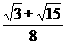
【解析】
(I)

(II)
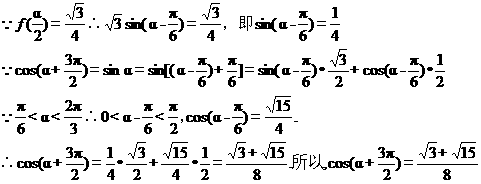
18.(本小题满分13分)
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字
是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)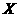 表示所取3张卡片上的数字的中位数,求
表示所取3张卡片上的数字的中位数,求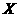 的分布列(注:若三个数
的分布列(注:若三个数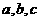 满足
满足
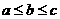 ,则称
,则称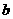 为这三个数的中位数).
为这三个数的中位数).
【答案】(I) 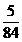 (II)
(II)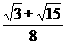
【解析】
(I)

(II)
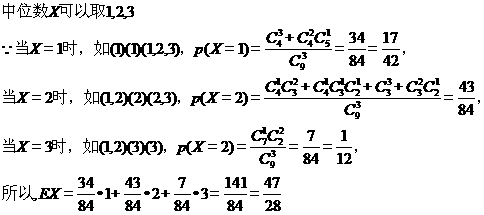
X的分布列如下:
x | 1 | 2 | 3 |
p |
|
|
|
19.(本小题满分12分)
如图(19),四棱锥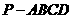 ,底面是以
,底面是以 为中心的菱形,
为中心的菱形, 底面
底面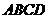 ,
,
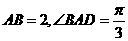 ,
,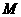 为
为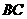 上一点,且
上一点,且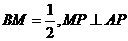 .
.
(1)求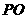 的长;
的长;
(2)求二面角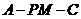 的正弦值。
的正弦值。
【答案】(I) 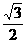 (II)
(II)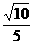
【解析】
(I)

(II)解析完成时间2014-6-12-qq-373780592

20.(本小题满分12分,(1)问4分,(2)问3分,(3)问5分)
已知函数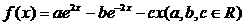 的导函数
的导函数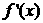 为偶函数,且曲线
为偶函数,且曲线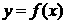 在点
在点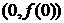 处的切线的斜率为
处的切线的斜率为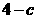 .
.
(1)确定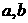 的值;
的值;
(2)若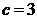 ,判断
,判断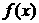 的单调性;
的单调性;
(3)若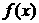 有极值,求
有极值,求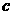 的取值范围.
的取值范围.
【答案】(1) a=b=1 (2)在R上单调递增 (3)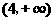
【解析】
(1)
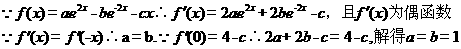
(2)解析完成时间2014-6-12-qq-373780592
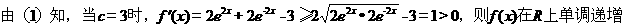
(3)解析完成时间2014-6-12-qq-373780592

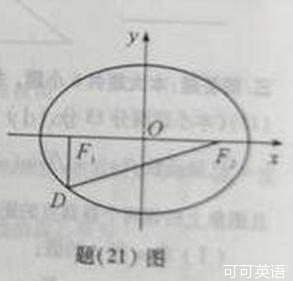
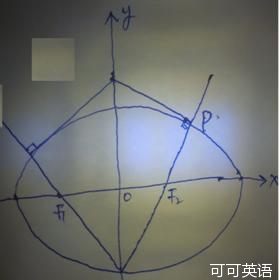
21.
如题(21)图,设椭圆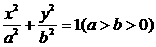 的左右焦点分别为
的左右焦点分别为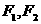 ,点
,点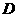 在椭圆上,
在椭圆上,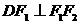 ,
,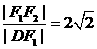 ,
,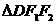 的面积为
的面积为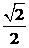 .
.
(1)求该椭圆的标准方程;
(2)是否存在圆心在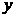 轴上的圆,使圆在
轴上的圆,使圆在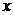 轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..
轴的上方与椭圆两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径..
【答案】(I) 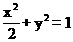 (II)
(II)
【解析】
(I)
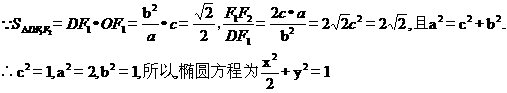
(II)解析完成时间2014-6-12-qq-373780592

22.(本小题满分12分,(1)问4分,(2)问8分)
设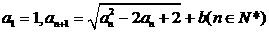
(1)若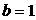 ,求
,求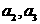 及数列
及数列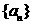 的通项公式;
的通项公式;
(2)若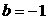 ,问:是否存在实数
,问:是否存在实数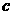 使得
使得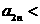 看不清
看不清
【答案】(I) 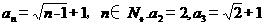 (II)
(II)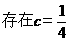
【解析】
(I)
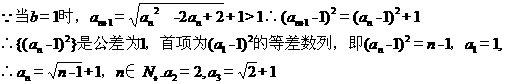
(II)解析完成时间2014-6-12-qq-373780592