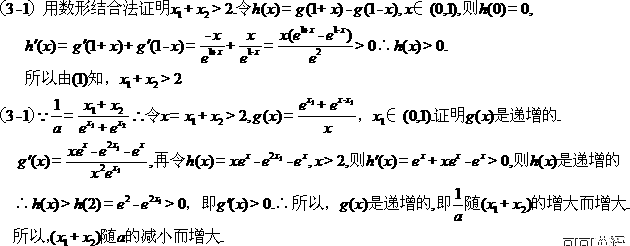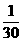第Ⅰ卷
一、选择题:在每小题给出的四个选项中只有一项是符合题目要求的.
(1)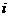 是虚数单位,复数
是虚数单位,复数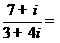 ( )
( )
(A)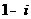 (B)
(B)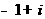 (C)
(C)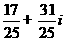 (D)
(D)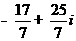
【答案】A
【解析】
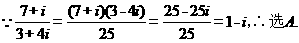
(2)设变量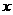 ,
,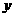 满足约束条件
满足约束条件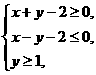 则目标函数
则目标函数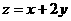 的最小值为( )
的最小值为( )
(A)2 (B)3 (C)4 (D)5
【答案】B
【解析】
此题区域不是封闭区域,属于陷阱题

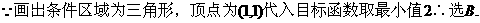
(3)阅读右边的程序框图,运行相应的程序,输出的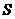 的值为( )
的值为( )
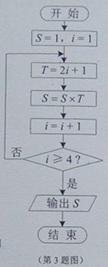
(A)15 (B)105
(C)245 (D)945
【答案】B
【解析】
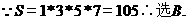
(4)函数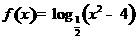 的单调递增区间是( )
的单调递增区间是( )
(A)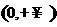 (B)
(B)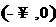
(C)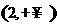 (D)
(D)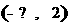
【答案】D
【解析】
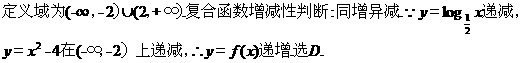
(5)已知双曲线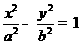
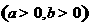 的一条渐近线平行于直线
的一条渐近线平行于直线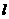 :
: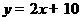 ,双曲线的一个焦点在直线
,双曲线的一个焦点在直线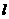 上,则双曲线的方程为( )
上,则双曲线的方程为( )
(A)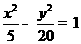 (B)
(B)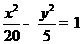
(C)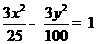 (D)
(D)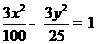
【答案】A
【解析】
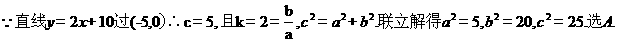
(6)如图,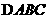 是圆的内接三角形,
是圆的内接三角形,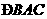 的平分线交圆于点
的平分线交圆于点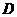 ,交
,交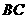 于点
于点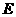 ,过点
,过点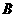 的圆的切线与
的圆的切线与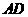 的延长线交于点
的延长线交于点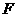 .在上述条件下,给出下列四个结论:①
.在上述条件下,给出下列四个结论:①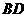 平分
平分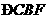 ;②
;②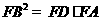 ;③
;③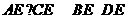 ;④
;④ .
.
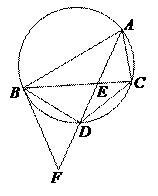
则所有正确结论的序号是( )
(A)①② (B)③④ (C)①②③ (D)①②④
【答案】D
【解析】

(7)设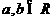 ,则|“
,则|“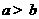 ”是“
”是“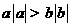 ”的( )
”的( )
(A)充要不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充要也不必要条件
【答案】C
【解析】

(8)已知菱形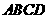 的边长为2,
的边长为2,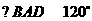 ,点
,点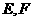 分别在边
分别在边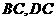 上,
上,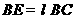 ,
,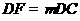 .若
.若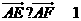 ,
,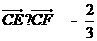 ,则
,则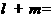 ( )
( )
(A)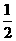 (B)
(B)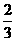 (C)
(C)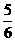 (D)
(D)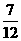
【答案】C
【解析】
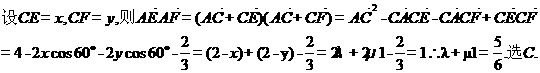
第Ⅱ卷
二、填空题(本大题共6个小题,每小题5分,共30分.把答案填在题中横线上.)
(9)某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生.
【答案】 60
【解析】
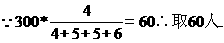
(10)已知一个几何体的三视图如图所示(单位:m),则该几何体的体积为_______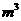 .
.
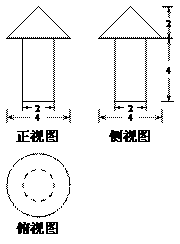
【答案】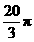
【解析】
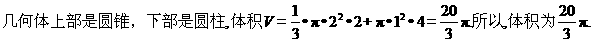
(11)设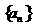 是首项为
是首项为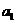 ,公差为-1的等差数列,
,公差为-1的等差数列,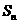 为其前
为其前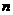 项和.若
项和.若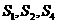 成等比数列,则
成等比数列,则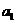 的值为__________.
的值为__________.
【答案】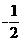
【解析】
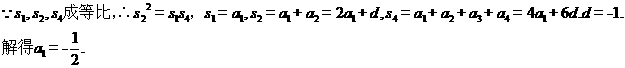
(12)在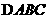 中,内角
中,内角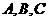 所对的边分别是
所对的边分别是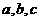 .已知
.已知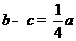 ,
,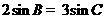 ,则
,则 的值为_______.
的值为_______.
【答案】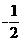
【解析】
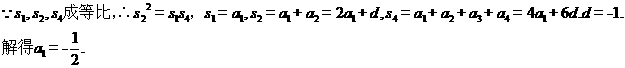
(B)在以 为极点的极坐标系中,圆
为极点的极坐标系中,圆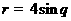 和直线
和直线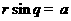 相交于
相交于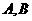 两点.若
两点.若 是等边三角形,则
是等边三角形,则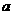 的值为___________.
的值为___________.
【答案】3
【解析】

(C)已知函数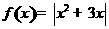 ,
,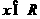 .若方程
.若方程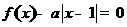 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数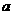 的取值范围为__________.
的取值范围为__________.
【答案】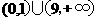
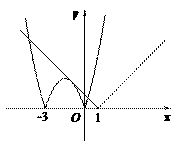
【解析】
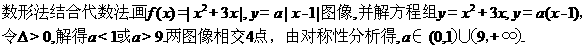
(15)(本小题满分13分)
已知函数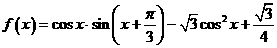 ,
,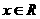 .
.
(Ⅰ)求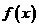 的最小正周期;
的最小正周期;
(Ⅱ)求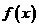 在闭区间
在闭区间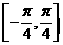 上的最大值和最小值.
上的最大值和最小值.
【答案】(1) 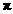 (2)
(2) 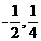
【解析】
(1)

(2)
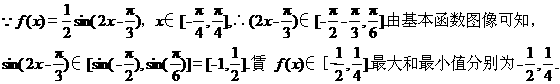
(16)(本小题满分13分)
某大学志愿者协会有6名男同学,4名女同学. 在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院. 现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(Ⅰ)求选出的3名同学是来自互不相同学院的概率;
(Ⅱ)设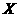 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量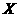 的分布列和数学期望.
的分布列和数学期望.
【答案】 (1) 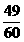 (2)
(2) 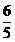
【解析】
(1)
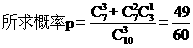
(2)
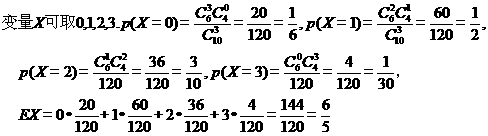
x | 0 | 1 | 2 | 3 |
p |
|
|
|
|
(17)(本小题满分13分)
如图,在四棱锥 中,
中,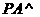 底面
底面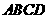 ,
,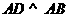 ,
,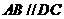 ,
,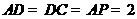 ,
,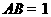 ,点
,点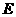 为棱
为棱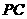 的中点.
的中点.
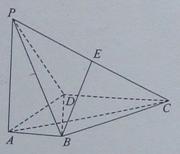
(Ⅰ)证明 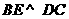 ;
;
(Ⅱ)求直线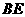 与平面
与平面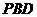 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若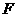 为棱
为棱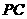 上一点,满足
上一点,满足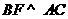 ,
,
求二面角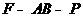 的余弦值.
的余弦值.
【答案】 (1) 省略 (2) 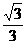 (3)
(3) 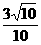
【解析】
(1)

(2)

(2)

(18)(本小题满分13分)
设椭圆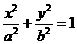 (
(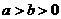 )的左、右焦点为
)的左、右焦点为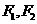 ,右顶点为
,右顶点为 ,上顶点为
,上顶点为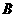 .已知
.已知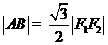 .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设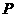 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段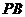 为直径的圆经过点
为直径的圆经过点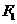 ,经过原点的直线
,经过原点的直线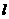 与该圆相切. 求直线的斜率.
与该圆相切. 求直线的斜率.
【答案】 (1) 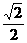 (2)
(2) 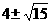
【解析】
(1)
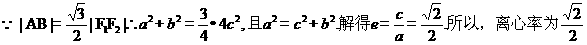
(2)

(19)(本小题满分14分)
已知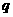 和
和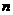 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合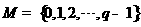 ,集合
,集合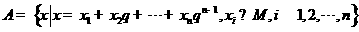 .
.
(Ⅰ)当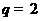 ,
,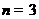 时,用列举法表示集合
时,用列举法表示集合 ;
;
(Ⅱ)设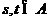 ,
,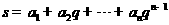 ,
,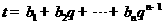 ,其中
,其中
【答案】 (1) {0,1,2,3,4,5,67} (2) 省略
【解析】
(1)
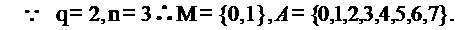
(2)
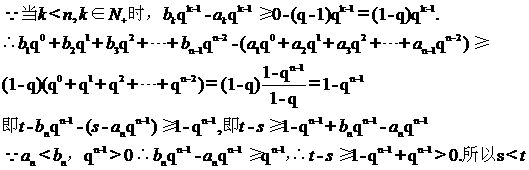
(20)(本小题满分14分)
已知函数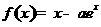
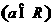 ,
,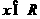 .已知函数
.已知函数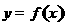 有两个零点
有两个零点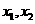 ,且
,且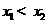 .
.
(Ⅰ)求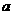 的取值范围;
的取值范围;
(Ⅱ)证明 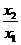 随着
随着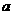 的减小而增大;
的减小而增大;
(Ⅲ)证明 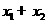 随着
随着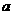 的减小而增大.
的减小而增大.
【答案】 (1) 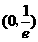 (2) 省略 (3) 省略
(2) 省略 (3) 省略
【解析】
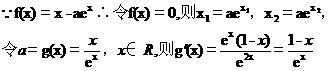
(1)

(2)
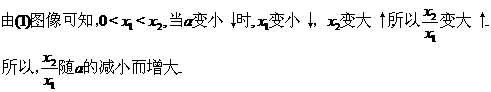
(3)