一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设复数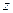 满足
满足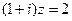 ,其中
,其中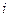 为虚数单位,则
为虚数单位,则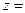
A.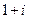 B.
B.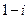 C.
C.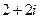 D.
D.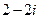
1.(B).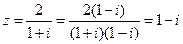
2.已知集合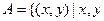 为实数,且
为实数,且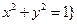 ,
,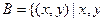 为实数,且
为实数,且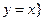 ,则
,则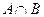 的元素个数为
的元素个数为
A.0 B.1 C.2 D.3
2.(C).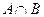 的元素个数等价于圆
的元素个数等价于圆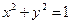 与直线
与直线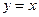 的交点个数,显然有2个交点
的交点个数,显然有2个交点
3.若向量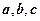 满足
满足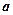 ∥
∥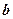 且
且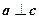 ,则
,则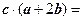
A.4 B.3 C.2 D.0
3.(D).依题意得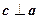 ,
,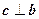 ,则
,则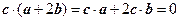
4.设函数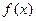 和
和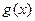 分别是
分别是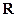 上的偶函数和奇函数,则下列结论恒成立的是
上的偶函数和奇函数,则下列结论恒成立的是
A.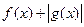 是偶函数 B.
是偶函数 B.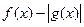 是奇函数
是奇函数
C.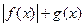 是偶函数 D.
是偶函数 D.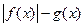 是奇函数
是奇函数
4.(A).由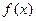 是偶函数、
是偶函数、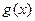 是奇函数,得
是奇函数,得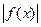 和
和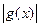 都是偶函数,所以
都是偶函数,所以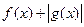 与
与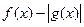 都是偶函数,
都是偶函数,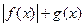 与
与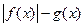 的奇偶性不能确定
的奇偶性不能确定
5.已知平面直角坐标系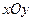 上的区域
上的区域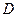 由不等式组
由不等式组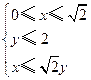 给定.若
给定.若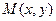 为
为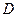 上的动点,点
上的动点,点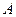
的坐标为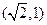 ,则
,则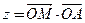 的最大值为
的最大值为
A.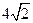 B.
B.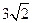 C.4 D.3
C.4 D.3
5.(C).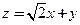 ,即
,即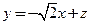 ,画出不等式组表示的平面区域,易知当直线
,画出不等式组表示的平面区域,易知当直线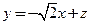 经过点
经过点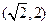 时,
时,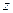 取得最大值,
取得最大值,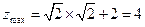
6.甲、乙两队进行排球决赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.
若两队胜每局的概率相同,则甲队获得冠军的概率为
A.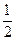 B.
B. C.
C.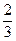 D.
D.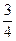
6.(D).乙获得冠军的概率为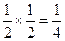 ,则甲队获得冠军的概率为
,则甲队获得冠军的概率为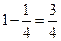
7.如图1 ~ 3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为

A.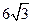 B.
B.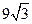 C.
C.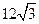 D.
D.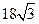
7.(B).该几何体是一个底面为平行四边形,高为3的四棱柱,易求得平行四边形的高为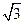 ,
,
则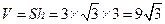
8.设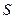 是整数集
是整数集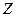 的非空子集,如果
的非空子集,如果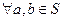 ,有
,有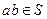 ,则称
,则称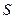 关于数的乘法是封闭的.若
关于数的乘法是封闭的.若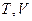 是
是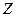
的两个不相交的非空子集,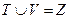 ,且
,且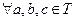 ,有
,有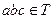 ;
;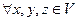 ,有
,有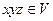 ,则下列结论恒成立的是
,则下列结论恒成立的是
A.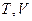 中至少有一个关于乘法是封闭的 B.
中至少有一个关于乘法是封闭的 B.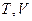 中至多有一个关于乘法是封闭的
中至多有一个关于乘法是封闭的
C.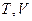 中有且只有一个关于乘法是封闭的 D.
中有且只有一个关于乘法是封闭的 D.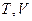 中每一个关于乘法都是封闭的
中每一个关于乘法都是封闭的
8.(A).若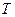 为奇数集,
为奇数集,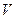 为偶数集,满足题意,此时
为偶数集,满足题意,此时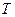 与
与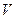 关于乘法都是封闭的,排除B、C
关于乘法都是封闭的,排除B、C
若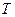 为负整数集,
为负整数集,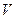 为非负整数集,也满足题意,此时只有
为非负整数集,也满足题意,此时只有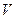 关于乘法是封闭的,排除D
关于乘法是封闭的,排除D
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
(一)必做题(9 ~ 13题)
9.不等式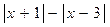 ≥0的解集是 .
≥0的解集是 .
9.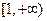 .
.
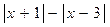 ≥0
≥0 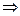
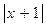 ≥
≥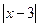
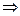
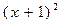 ≥
≥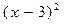
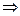
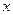 ≥1
≥1
10.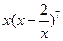 的展开式中,
的展开式中,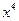 的系数是 (用数字作答)
的系数是 (用数字作答)
10.84.
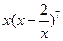 的通项
的通项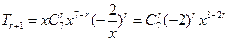 ,由
,由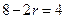 得
得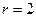 ,则
,则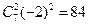
11.等差数列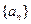 前9项的和等于前4项的和.若
前9项的和等于前4项的和.若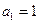 ,
,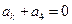 ,则
,则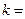 .
.
11.10.
方法1:由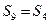 得
得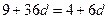 ,求得
,求得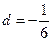 ,则
,则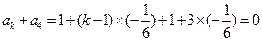 ,解得
,解得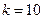
方法2:由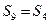 得
得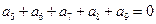 ,即
,即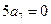 ,
,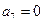 ,即
,即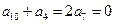 ,即
,即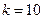
12.函数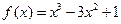 在
在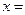 处取得极小值.
处取得极小值.
12.2.
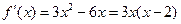 ,令
,令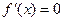 得
得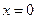 或
或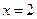 ,显然当
,显然当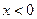 时
时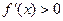 ;
;
当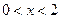 时
时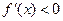 ;当
;当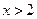 时
时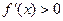 ,函数
,函数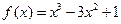 在
在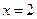 处取得极小值
处取得极小值
13.某数学老师身高176cm,他爷爷、父亲和儿子的身高分别是173cm、170cm和182cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为 cm.
13.185.
设父亲的身高为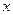 cm,儿子的身高为
cm,儿子的身高为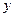 cm,则根据上述数据可得到如下表格:
cm,则根据上述数据可得到如下表格:
| 173 | 170 | 176 | 182 |
| 170 | 176 | 182 | ? |
上表中的最后一组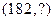 是预测数据,
是预测数据,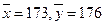
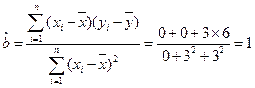 ,
,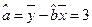
线性回归方程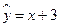 ,所以当
,所以当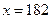 时,
时,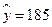 ,即他孙子的预测身高为185 cm.
,即他孙子的预测身高为185 cm.
(二)选做题(14 ~ 15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)已知两曲线参数方程分别为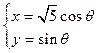
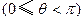 和
和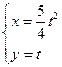
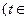
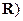 ,它们的交点坐标为___________.
,它们的交点坐标为___________.
14.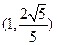 .
.
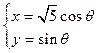 表示椭圆
表示椭圆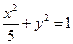
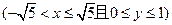 ,
,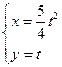 表示抛物线
表示抛物线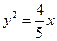
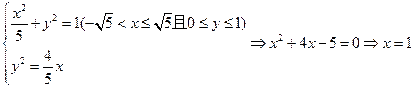 或
或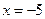 (舍去),
(舍去),
又因为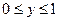 ,所以它们的交点坐标为
,所以它们的交点坐标为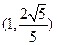
15.(几何证明选讲选做题)如图4,过圆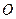 外一点
外一点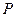 分别作圆的切线和割线交圆于
分别作圆的切线和割线交圆于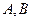 ,且
,且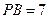 ,
,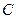 是圆上一点使得
是圆上一点使得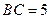 ,
,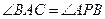 ,则
,则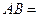 ___________.
___________.
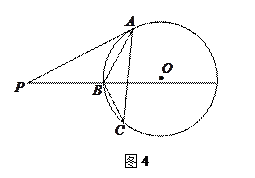
15.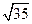 .
.
由弦切角定理得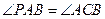 ,又
,又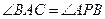 ,
,
则△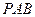 ∽△
∽△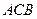 ,则
,则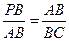 ,
,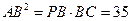 ,即
,即