评论
打印
一、填空题（本大题共有14题，满分56分）考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.
1.不等式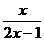
＜0的解为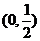 
.
【答案】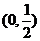
【解析】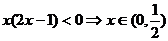
2.在等差数列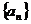
中，若a1+ a2+ a3+ a4=30，则a2+ a3= 15 .
【答案】 15
【解析】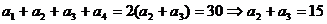 
3.设m∈R,m2+m-2+( m2-1)i是纯虚数，其中i是虚数单位，则m= .
【答案】 -2
【解析】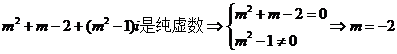 
4.已知
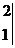=0，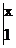
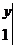=1，则y= 1 .
【答案】 1
【解析】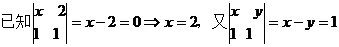
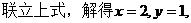
5.已知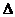
ABC的内角A、B、C所对的边分别是a、b、c.若a2+ab+b2-c2=0，则角C的大小是
.
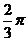【答案】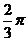
【解析】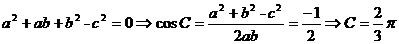
6.某学校高一年级男生人数占该年级学生人数的40%.在一次考试中，男、女生平均分数分别是75、80，则这次考试该年级学生平均分数为 78 .
【答案】 78
【解析】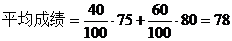 
7.设常数a∈R.若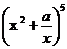
的二项展开式中x7项的系数为-10，则a= -2 .
【答案】 -2
【解析】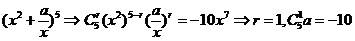
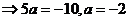
8.方程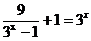
的实数解为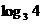 
.
【答案】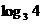
【解析】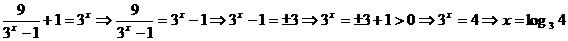
9.若cosxcosy+sinxsiny=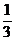
，则cos(2x-2y)= 
.
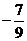【答案】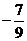
【解析】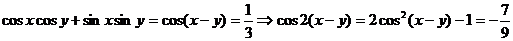 
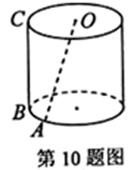
10.已知圆柱
的母线长为l，底面半径为r,O是上底面圆心，A、B是下底面圆周上的两个不同的点，BC是母线，如图.若直线OA与BC所成角的大小为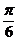
，则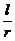
= 
.
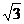【答案】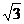
【解析】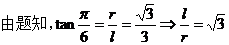 
11.盒子中装有编号为1，2，3，4，5，6，7的七个球，从中任意取出两个，则这两个球的编号之积为偶数的概率是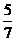 
（结果用最简分数表示）.
【答案】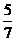
【解析】考查排列组合；概率计算策略：正难则反。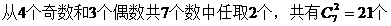
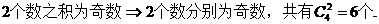
12.设AB是椭圆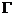
的长轴，点C在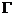上，且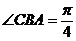
.若AB=4，BC=
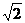，则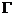的两个焦点之间的距离为 
.
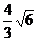【答案】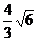
【解析】 如右图所示。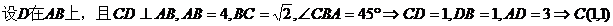
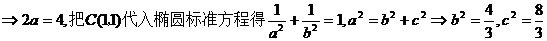
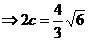
13.设常数a＞0.若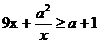
对一切正实数x成立，则a的取值范围为 
.
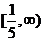【答案】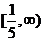
【解析】 考查均值不等式的应用。
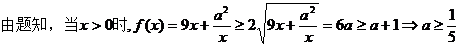
14.已知正方形ABCD的边长为1.记以A为起点，其余顶点为终点的向量分别为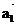
、
、
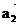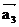；以C为起点，其余顶点为终点的向量分别为
、
、
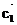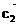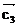.若i,j,k,l∈
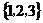且i≠j,k≠l，则
·
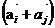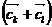的最小值是 -5 .
【答案】 -5
【解析】 根据对称性，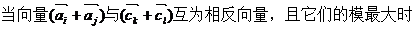
。
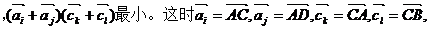
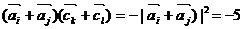