第Ⅰ卷
一、 选择题共12小题。每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1、已知集合A={x|x2-2x>0},B={x|-<x<},则 ( )
A、A∩B=Æ B、A∪B=R C、B⊆A D、A⊆B
【命题意图】本题主要考查一元二次不等式解法、集合运算及集合间关系,是容易题.
【解析】A=(-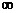 ,0)∪(2,+
,0)∪(2,+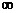 ), ∴A∪B=R,故选B.
), ∴A∪B=R,故选B.
2、若复数z满足 (3-4i)z=|4+3i |,则z的虚部为 ( )
A、-4 (B)- (C)4 (D)
【命题意图】本题主要考查复数的概念、运算及复数模的计算,是容易题.
【解析】由题知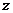 =
=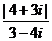 =
=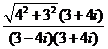 =
=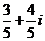 ,故z的虚部为
,故z的虚部为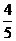 ,故选D.
,故选D.
3、为了解某地区的中小学生视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大,在下面的抽样方法中,最合理的抽样方法是 ( )
A、简单随机抽样 B、按性别分层抽样 C、按学段分层抽样 D、系统抽样
【命题意图】本题主要考查分层抽样方法,是容易题.
【解析】因该地区小学、初中、高中三个学段学生的视力情况有较大差异,故最合理的抽样方法是按学段分层抽样,故选C.
4、已知双曲线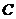 :
: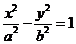 (
(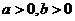 )的离心率为
)的离心率为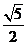 ,则
,则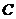 的渐近线方程为
的渐近线方程为
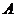 .
.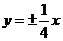
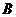 .
.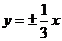
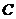 .
.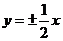
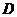 .
.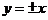
【命题意图】本题主要考查双曲线的几何性质,是简单题.
【解析】由题知,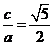 ,即
,即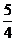 =
=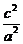 =
=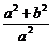 ,∴
,∴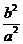 =
=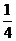 ,∴
,∴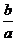 =
=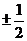 ,∴
,∴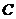 的渐近线方程为
的渐近线方程为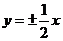 ,故选
,故选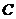 .
.
5、运行如下程序框图,如果输入的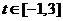 ,则输出s属于
,则输出s属于

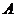 .[-3,4]
.[-3,4] 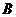 .[-5,2]
.[-5,2] 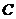 .[-4,3]
.[-4,3] 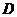 .[-2,5]
.[-2,5]
【命题意图】本题主要考查程序框图及分段函数值域求法,是简单题.
【解析】有题意知,当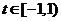 时,
时,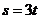
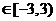 ,当
,当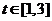 时,
时,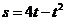
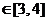 ,
,
∴输出s属于[-3,4],故选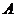 .
.
6、如图,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为 ( )

A、cm3 B、cm3
C、cm3 D、cm3
【命题意图】本题主要考查球的截面圆性质、球的体积公式,是容易题.
【解析】设球的半径为R,则由题知球被正方体上面截得圆的半径为4,球心到截面圆的距离为R-2,则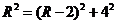 ,解得R=5,∴球的体积为
,解得R=5,∴球的体积为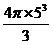 =
=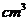 ,故选A.
,故选A.
7、设等差数列{an}的前n项和为Sn,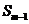 =-2,
=-2,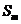 =0,
=0,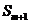 =3,则
=3,则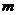 = ( )
= ( )
A、3 B、4 C、5 D、6
【命题意图】本题主要考查等差数列的前n项和公式及通项公式,考查方程思想,是容易题.
【解析】有题意知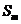 =
=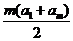 =0,∴
=0,∴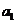 =-
=-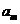 =-(
=-(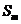 -
-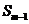 )=-2,
)=-2,
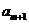 =
= 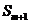 -
-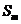 =3,∴公差
=3,∴公差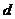 =
=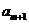 -
-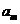 =1,∴3=
=1,∴3=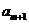 =-
=-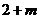 ,∴
,∴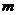 =5,故选C.
=5,故选C.
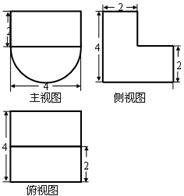
8、某几何体的三视图如图所示,则该几何体的体积为
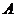 .
.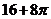
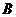 .
.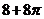
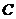 .
.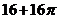
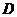 .
.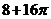
【命题意图】本题主要考查简单组合体的三视图及简单组合体体积公式,是中档题.
【解析】由三视图知,该几何体为放到的半个圆柱底面半径为2高为4,上边放一个长为4宽为2高为2长方体,故其体积为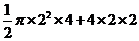 =
=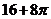 ,故选
,故选 .
.
9、设m为正整数,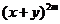 展开式的二项式系数的最大值为
展开式的二项式系数的最大值为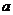 ,
,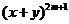 展开式的二项式系数的最大值为
展开式的二项式系数的最大值为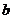 ,若13
,若13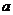 =7
=7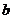 ,则
,则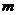 = ( )
= ( )
A、5 B、6 C、7 D、8
【命题意图】本题主要考查二项式系数最大值及组合数公式,考查方程思想,是容易题.
【解析】由题知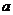 =
=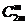 ,
,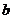 =
=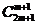 ,∴13
,∴13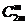 =7
=7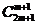 ,即
,即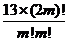 =
=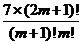 ,
,
解得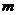 =6,故选B.
=6,故选B.
10、已知椭圆+=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点。若AB的中点坐标为(1,-1),则E的方程为 ( )
A、+=1 B、+=1 C、+=1 D、+=1
【命题意图】本题主要考查椭圆中点弦的问题,是中档题.
【解析】设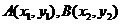 ,则
,则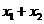 =2,
=2,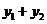 =-2,
=-2,
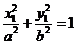 ①
① 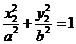 ②
②
①-②得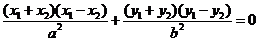 ,
,
∴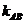 =
=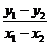 =
=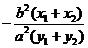 =
=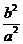 ,又
,又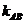 =
=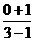 =
=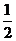 ,∴
,∴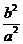 =
=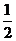 ,又9=
,又9=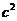 =
=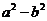 ,解得
,解得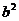 =9,
=9,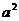 =18,∴椭圆方程为
=18,∴椭圆方程为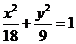 ,故选D.
,故选D.
11、已知函数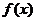 =
=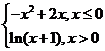 ,若|
,若|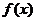 |≥
|≥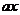 ,则
,则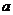 的取值范围是
的取值范围是
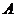 .
.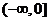
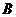 .
.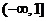
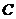 .[-2,1]
.[-2,1] 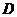 .[-2,0]
.[-2,0]
【命题意图】本题主要考查函数不等式恒成立求参数范围问题的解法,是难题。
【解析】∵|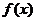 |=
|=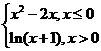 ,∴由|
,∴由|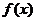 |≥
|≥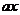 得,
得,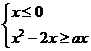 且
且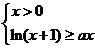 ,
,
由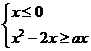 可得
可得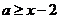 ,则
,则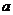 ≥-2,排除A,B,
≥-2,排除A,B,
当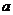 =1时,易证
=1时,易证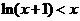 对
对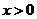 恒成立,故
恒成立,故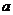 =1不适合,排除C,故选D.
=1不适合,排除C,故选D.
12、设△AnBnCn的三边长分别为an,bn,cn,△AnBnCn的面积为Sn,n=1,2,3,…
若b1>c1,b1+c1=2a1,an+1=an,bn+1=,cn+1=,则( )
A、{Sn}为递减数列 B、{Sn}为递增数列
C、{S2n-1}为递增数列,{S2n}为递减数列
D、{S2n-1}为递减数列,{S2n}为递增数列
【命题意图】
【解析】B











