一.选择题选择题:本大题共10小题。每小题5分,共50分。在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)设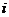 是虚数单位,若复数
是虚数单位,若复数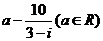 是纯虚数,则
是纯虚数,则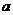 的值为 ( )
的值为 ( )
(A)-3 (B)-1 (C)1 (D)3
【答案】D
【解析】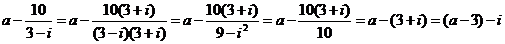 ,所以a=3,
,所以a=3,
故选择D
【考点定位】考查纯虚数的概念,及复数的运算,属于简单题.
(2)已知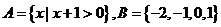 ,则
,则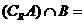 ( )
( )
(A)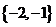 (B)
(B)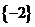
(C)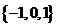 (D)
(D)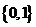
【答案】A
【解析】A: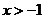 ,
,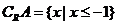 ,
,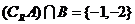 ,所以答案选A
,所以答案选A
【考点定位】考查集合的交集和补集,属于简单题.
(3)如图所示,程序据图(算法流程图)的输出结果为
(A)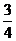 (B)
(B)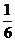
(C)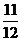 (D)
(D)
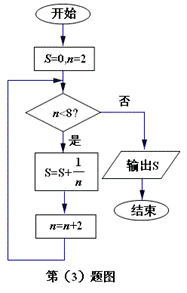
【答案】C
【解析】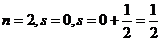 ;
;
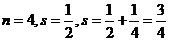 ;
;
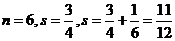
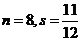 ,输出
,输出
所以答案选择C
【考点定位】本题考查算法框图的识别,逻辑思维,属于中等难题.
(4)“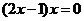 ”是“
”是“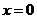 ”的
”的
(A)充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
【答案】B
【解析】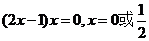 ,所以答案选择B
,所以答案选择B
【考点定位】考查充分条件和必要条件,属于简单题.
(5)若某公司从五位大学毕业生甲、乙、丙、丁、戌中录用三人,这五人被录用的机会均等,则甲或乙被
录用的概率为
(A)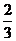 (B)
(B) 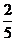
(C) 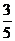 (D)
(D)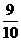
【答案】D
【解析】总的可能性有10种,甲被录用乙没被录用的可能性3种,乙被录用甲没被录用的可能性3种,甲乙都被录用的可能性3种,所以最后的概率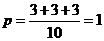
【考点定位】考查古典概型的概念,以及对一些常见问题的分析,简单题.
(6)直线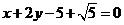 被圆
被圆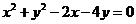 截得的弦长为
截得的弦长为
(A)1 (B)2
(C)4 (D)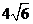
【答案】C
【解析】圆心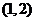 ,圆心到直线的距离
,圆心到直线的距离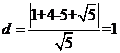 ,半径
,半径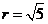 ,所以最后弦长为
,所以最后弦长为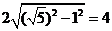 .
.
【考点定位】考查解析几何初步知识,直线与圆的位置关系,点到直线的距离,简单题.
(7)设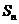 为等差数列
为等差数列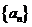 的前
的前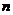 项和,
项和,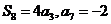 ,则
,则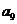 =
=
(A)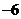 (B)
(B)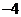
(C)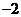 (D)2
(D)2
【答案】A
【解析】
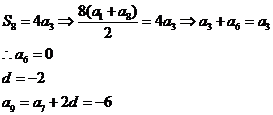
【考点定位】考查等差数列通项公式和前n项公式的应用,以及数列基本量的求解.
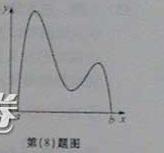
(8) 函数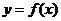 的图像如图所示,在区间
的图像如图所示,在区间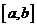 上可找到
上可找到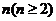 个不同的数
个不同的数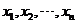 ,使得
,使得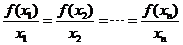 ,则
,则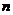 的取值范围为
的取值范围为
(A) 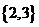 (B)
(B) 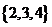
(C) 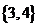 (D)
(D) 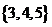
【答案】B
【解析】
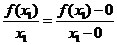 表示
表示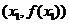 到原点的斜率;
到原点的斜率;
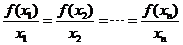 表示
表示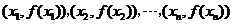 与原点连线的斜率,而
与原点连线的斜率,而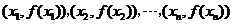 在曲线图像上,故只需考虑经过原点的直线与曲线的交点有几个,很明显有3个,故选B.
在曲线图像上,故只需考虑经过原点的直线与曲线的交点有几个,很明显有3个,故选B.
【考点定位】考查数学中的转化思想,对函数的图像认识.
(9) 设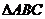 的内角
的内角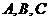 所对边的长分别为
所对边的长分别为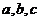 ,若
,若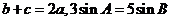 ,则角
,则角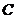 =
=
(A) 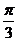 (B)
(B) 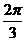
(C) 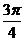 (D)
(D) 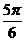
【答案】B
【解析】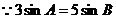 由正弦定理,所以
由正弦定理,所以 ;
;
因为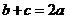 ,所以
,所以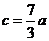 ,
,
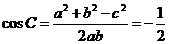 ,所以
,所以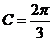 ,答案选择B
,答案选择B
【考点定位】考查正弦定理和余弦定理,属于中等难度.
(10)已知函数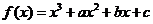 有两个极值点
有两个极值点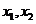 ,若
,若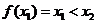 ,则关于
,则关于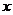 的方程
的方程
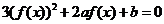 的不同实根个数为
的不同实根个数为
(A)3 (B) 4
(C) 5 (D) 6
【答案】A
【解析】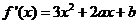 ,
,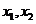 是方程
是方程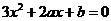 的两根,
的两根,
由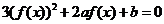 ,则又两个
,则又两个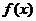 使得等式成立,
使得等式成立,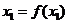 ,
,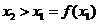 ,其函数图象如下:
,其函数图象如下:
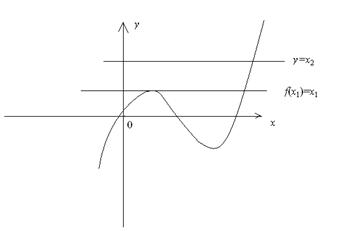
如图则有3个交点,故选A.
【考点定位】考查函数零点的概念,以及对嵌套型函数的理解.











