第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 设 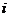 是虚数单位,复数
是虚数单位,复数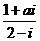 为纯虚数,则实数a 为
为纯虚数,则实数a 为
(A)2(B) 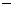 2 (C)
2 (C) 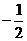 (D)
(D)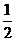
(1)A【命题意图】本题考查复数的基本运算,属简单题.
【解析】设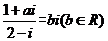 ,则
,则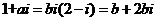 ,所以
,所以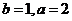 .故选A.
.故选A.
(2) 双曲线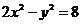 的实轴长是
的实轴长是
(A)2 (B)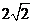 (C) 4 (D) 4
(C) 4 (D) 4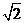
(2)C【命题意图】本题考查双曲线的标准方程,考查双曲线的性质.属容易题.
【解析】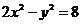 可变形为
可变形为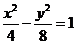 ,则
,则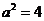 ,
,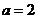 ,
,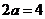 .故选C.
.故选C.
(3) 设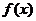 是定义在
是定义在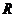 上的奇函数,当
上的奇函数,当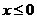 时,
时,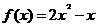 ,则
,则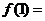
(A)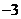 (B)
(B) 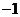 (C)1 (D)3
(C)1 (D)3
(3)A【命题意图】本题考查函数的奇偶性,考查函数值的求法.属容易题.
【解析】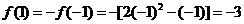 .故选A.
.故选A.
(4)设变量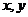 满足
满足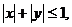 则
则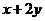 的最大值和最小值分别为
的最大值和最小值分别为
(A)1,-1 (B)2,-2 (C)1,-2 (D)2,-1
(4)B【命题意图】本题考查线性规划问题.属容易题.
【解析】不等式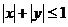 对应的区域如图所示,
对应的区域如图所示,
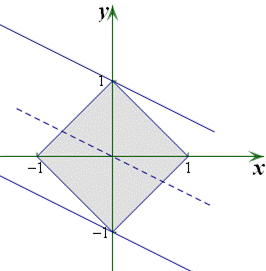
当目标函数过点(0,-1),(0,1)时,分别取最小或最大值,所以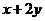 的最大值和最小值分别为2,-2.故选B.
的最大值和最小值分别为2,-2.故选B.
(5) 在极坐标系中,点 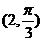 到圆
到圆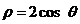 的圆心的距离为
的圆心的距离为
(A)2(B) 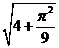 (C)
(C) 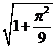 (D)
(D) 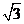
(5)D【命题意图】本题考查极坐标的知识及极坐标与直角坐标的相互转化,考查两点间距离.
【解析】极坐标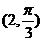 化为直角坐标为
化为直角坐标为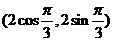 ,即
,即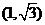 .圆的极坐标方程
.圆的极坐标方程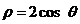 可化为
可化为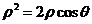 ,化为直角坐标方程为
,化为直角坐标方程为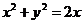 ,即
,即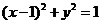 ,所以圆心坐标为(1,0),则由两点间距离公式
,所以圆心坐标为(1,0),则由两点间距离公式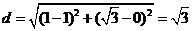 .故选D.
.故选D.
(6)一个空间几何体得三视图如图所示,则该几何体的表面积为
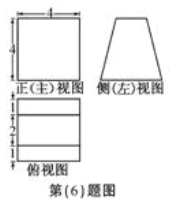
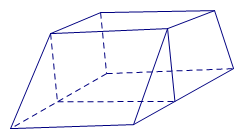
第(8)题图
(A) 48 (B)32+8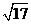 (C) 48+8
(C) 48+8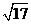 (D) 80
(D) 80
(6)C【命题意图】本题考查三视图的识别以及空间多面体表面积的求法.
【解析】由三视图可知几何体是底面是等腰梯形的直棱柱.底面等腰梯形的上底为2,下底为4,高为4,两底面积和为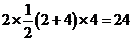 ,四个侧面的面积为
,四个侧面的面积为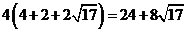 ,所以几何体的表面积为
,所以几何体的表面积为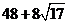 .故选C.
.故选C.
(7)命题“所有能被2整除的数都是偶数”的否定是
(A)所有不能被2整除的数都是偶数
(B)所有能被2整除的数都不是偶数
(C)存在一个不能被2整除的数是偶数
(D)存在一个能被2整除的数不是偶数
(7)D【命题意图】本题考查全称命题的否定.属容易题.
【解析】把全称量词改为存在量词,并把结果否定.
(8)设集合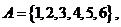
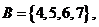 则满足
则满足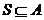 且
且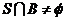 的集合
的集合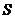 的个数为
的个数为
(A)57 (B)56 (C)49 (D)8
(8)B【命题意图】本题考查集合间的基本关系,考查集合的基本运算,考查子集问题,考查组合知识.属中等难度题.
【解析】集合A的所有子集共有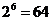 个,其中不含4,5,6,7的子集有
个,其中不含4,5,6,7的子集有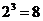 个,所以集合
个,所以集合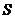 共有56个.故选B.
共有56个.故选B.
(9)已知函数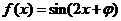 ,其中
,其中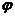 为实数,若
为实数,若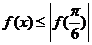 对
对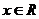 恒成立,且
恒成立,且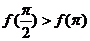 ,则
,则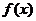 的单调递增区间是
的单调递增区间是
(A)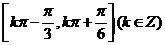 (B)
(B)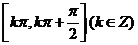
(C)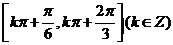 (D)
(D)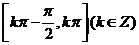
(9)C【命题意图】本题考查正弦函数的有界性,考查正弦函数的单调性.属中等偏难题.
【解析】若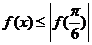 对
对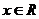 恒成立,则
恒成立,则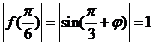 ,所以
,所以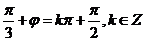 ,
,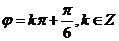 .由
.由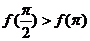 ,(
,(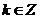 ),可知
),可知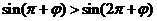 ,即
,即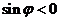 ,所以
,所以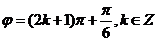 ,代入
,代入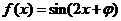 ,得
,得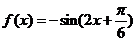 ,由
,由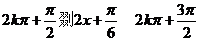 ,得
,得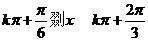 ,故选C.
,故选C.
(10) 函数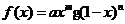 在区间〔0,1〕上的图像如图所示,则m,n的值可能是
在区间〔0,1〕上的图像如图所示,则m,n的值可能是
(A)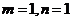 (B)
(B) 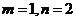
(C) 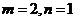 (D)
(D) 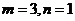
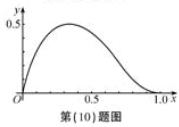
(10)B【命题意图】本题考查导数在研究函数单调性中的应用,考查函数图像,考查思维的综合能力.难度大.
【解析】代入验证,当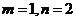 ,
,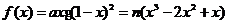 ,则
,则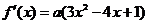 ,由
,由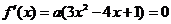 可知,
可知,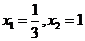 ,结合图像可知函数应在
,结合图像可知函数应在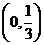 递增,在
递增,在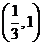 递减,即在
递减,即在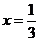 取得最大值,由
取得最大值,由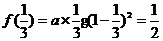 ,知a存在.故选B.
,知a存在.故选B.
第II卷(非选择题 共100分)
考生注意事项:
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.











