一、选择题:本大题共9小题,每小题5分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数z=i·(1+i)(i为虚数单位)在复平面上对应的点位于___ B ____
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】B
【解析】 z = i·(1+i) = i – 1.所以对应点(-1,1).选B
2.“1<x<2”是“x<2”成立的___ A ____
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】A
【解析】 若“1<x<2”成立,则“x<2”成立,所以“1<x<2”是“x<2”的充分条件;
若“x<2” 成立,则“1<x<2”不一定成立, 所以“1<x<2”不是“x<2”的必要条件.
综上,“1<x<2”是“x<2”的充分不必要条件.
选A
3.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件。为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=___ D ____
A.9 B.10 C.12 D.13
【答案】D
【解析】 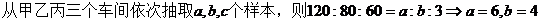
n = a + b + c=13.
选D
4.已知f(x)是奇函数,g(x)是偶函数,且f(-1)+g(1)=2,f(1)+g(-1)=4,则g(1)等于____ B ____
A.4 B.3 C.2 D.1
【答案】 B
【解析】 由题知f(-1)+g(1)= - f(1)+g(1)= 2,
f(1)+g(-1)= f(1)+ g(1)= 4.上式相加,解得g(1) = 3 .
选B
5.在锐角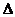 ABC中,角A,B所对的边长分别为a,b. 若2sinB=
ABC中,角A,B所对的边长分别为a,b. 若2sinB=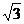 b,则角A等于____ A ____
b,则角A等于____ A ____
A.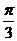 B.
B.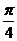 C.
C.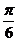 D.
D.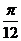
【答案】 A
【解析】 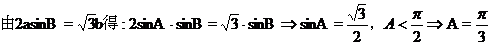
选A
6.函数f(x)=㏑x的图像与函数g(x)=x2-4x+4的图像的交点个数为____ C ____
A.0 B.1 C.2 D.3
【答案】 C
【解析】 在同一坐标系中画出对数函数f(x)=㏑x的图像和二次函数g(x)=x2-4x+4的图像,观察可知交点个数为2个。
选C
7.已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为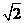 的矩形,则该正方体的正视图的面积等于____ D ____
的矩形,则该正方体的正视图的面积等于____ D ____
A. 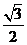 B.1 C.
B.1 C.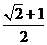 D.
D.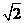
【答案】 D
【解析】 正方体的侧视图面积为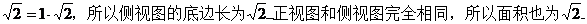 选D
选D
8.已知a,b是单位向量,a·b=0.若向量c满足|c-a-b|=1,则|c|的最大值为____ C ____
A.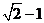 B.
B.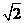 C.
C.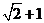 D.
D.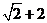
【答案】 C
【解析】  可以这样认为:在直角坐标系中,
可以这样认为:在直角坐标系中, 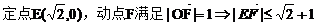
选C
9.已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为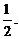 ,则
,则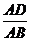 =____ D ____
=____ D ____
A.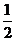 B.
B.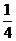 C.
C.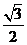 D.
D.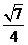
【答案】 D
【解析】 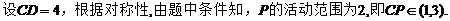
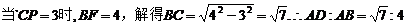
选D
二、填空题:本大题共6小题,每小题5分,共30分。
10.已知集合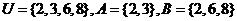 ,则
,则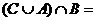 __
__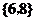 ___
___
【答案】 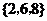
【解析】 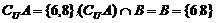 .
.
11.在平面直角坐标系xOy中,若直线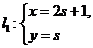 (s为参数)和直线
(s为参数)和直线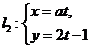 (t为参数)平行,则常数a的值为___4___
(t为参数)平行,则常数a的值为___4___
【答案】 4
【解析】 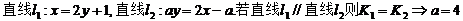 .
.
12.执行如图1所示的程序框图,如果输入a=1,b=2,则输出的a的值为____9___
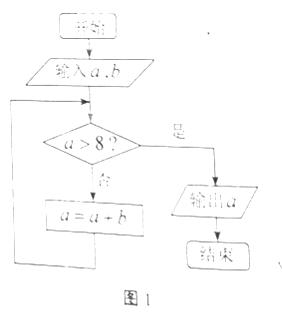
【答案】 4
【解析】 a = a + b + b + b…… = 1+2+2+2+2=9.
13.若变量x,y满足约束条件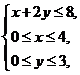 则x+y的最大值为___6___
则x+y的最大值为___6___
【答案】 6
【解析】 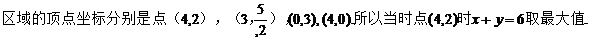
14.设F1,F2是双曲线C,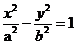 (a>0,b>0)的两个焦点。若在C上存在一点P。使
(a>0,b>0)的两个焦点。若在C上存在一点P。使
PF1⊥PF2,且∠PF1F2=30°,则C的离心率为____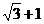 _______.
_______.
【答案】 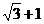
【解析】 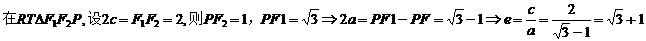
15.对于E={a1,a2,….a100}的子集X={a1,a2,…,an},定义X的“特征数列”
为x1,x2…,x100,其中x1=x10=…xn=1.其余项均为0,例如子集{a2,a3}的
“特征数列”为0,1,0,0,…,0
(1) 子集{a1,a3,a5}的“特征数列”的前三项和等于_____2________;
(2) 若E的子集P的“特征数列”P1,P2,…,P100 满足P1+Pi+1=1, 1≤i≤99;
E 的子集Q的“特征数列” q1,q2,q100 满足q1=1,q1+qj+1+qj+2=1,
1≤j≤98,则P∩Q的元素个数为___17______.
【答案】 (1) 2 (2)
【解析】 (1) 由题知,特征数列为:1,0,1,0,1,0,0,0……0.所以前3项和 = 2。
(2) P的“特征数列”:1,0,1,0 … 1,0. 所以P = 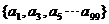 .
.
Q的“特征数列”:1,0,0,1,0,0 …1,0,0,1. 所以Q = 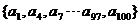 .
.
所以, 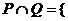
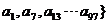 ,共有17个元素。
,共有17个元素。











