一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.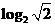 的值为 【 D 】
的值为 【 D 】
A.-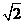 B.
B. 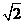 C.
C. 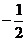 D.
D. 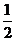
2. 抛物线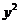 =-8x的焦点坐标是 【 B 】
=-8x的焦点坐标是 【 B 】

A.(2,0) B. (- 2,0) C. (4,0) D. (- 4,0)
3.设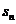 是等差数列{
是等差数列{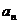 }的前n项和,已知
}的前n项和,已知 =3,
=3,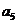 =11,则
=11,则 等于 【 C 】
等于 【 C 】
A.13 B. 35 C. 49 D. 63

4.如图1 D,E,F分别是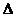 ABC的边AB,BC,CA的中点,则 【 A 】
ABC的边AB,BC,CA的中点,则 【 A 】
A.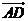 +
+  +
+  =0
=0
B.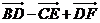 =0
=0

C.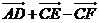 =0
=0
D. =0 图1
=0 图1
5.某地政府召集5家企业的负责人开会,其中甲企业有2人到会,其余4家企业各有1人到会,会上有3人发言,则这3人来自3家不同企业的可能情况的种数为【 B 】
A.14 B. 16 C. 20 D. 48
6.平面六面体 -
- 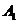
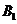
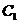
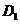 中,既与
中,既与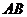 共面也与
共面也与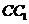 共面的棱的条数为【 C 】
共面的棱的条数为【 C 】
A.3 B. 4 C.5 D. 6

7.若函数y=f(x)导函数在区间[a,b]是增函数,则函数y=f(x)在区间[a,b]上的图象可能是(A)

8. 设函数 在
在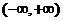 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数


取函数 。当
。当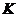 =
=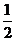 时,函数
时,函数 的单调递增区间为 【C】
的单调递增区间为 【C】
A  B
B 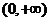 C
C  D
D 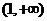
二 填空题:本大题共七小题,没小题5分,共35分,把答案填在答题卡中对应题号后的横线上。
9 . 某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 .
10. 若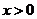 ,则
,则 的最小值为
的最小值为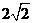 .
.
11. 在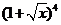 的展开式中,
的展开式中,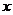 的系数为 6 (用数字作答)。
的系数为 6 (用数字作答)。
12 . 一个总体分为A.B两层,用分层抽样方法从总体中抽取一个容量为10的样本。已知B层中每个个体被抽到的概率都为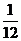 ,则总体中的个体数为 120
,则总体中的个体数为 120
13. 过双曲线C:
 的一个焦点作圆
的一个焦点作圆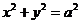 的两条切线,切点分别为A.B,若
的两条切线,切点分别为A.B,若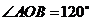 (O是坐标原点),则双曲线线C的离心率为 2 。
(O是坐标原点),则双曲线线C的离心率为 2 。
14. 在锐角 中,
中, 则
则 的值等于 2 ,
的值等于 2 ,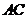 的取值范围为
的取值范围为 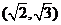 。
。
15. 如图2,两块斜边长相等的直角三角板在一起,若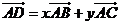 ,则
,则
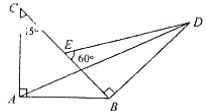
 ,
,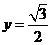 .
. 

图2
三 解答题:每小题共6小题,共75分,解答应写出文字说明.证明过程或演算步骤。
 16 (每小题满分12分)
16 (每小题满分12分)
以知向量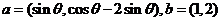 。
。
(Ⅰ)若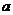 //
//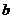 ,求
,求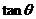 的值;
的值;
(Ⅱ)若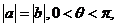 求
求 的值。
的值。

解(Ⅰ) 因为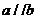 ,所以
,所以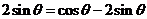 ,于是
,于是  ,故tan
,故tan =
=
(Ⅱ)由 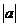 =
=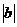 知,
知,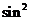
 +(cos
+(cos -2sin
-2sin
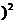 =5,所以
=5,所以
1-2sin2 +4
+4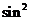
 =5.
=5.
从而-2sin2 +2(1-cos2
+2(1-cos2 =4,即sin2
=4,即sin2 +cos2
+cos2 = -1,于是
= -1,于是
Sin(2 +
+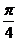 )= -
)= - 
又由0< <
<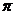 知,
知, 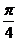 <2
<2 +
+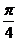 <
<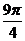 ,所以2
,所以2 +
+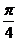 =
= ,或2
,或2 -
-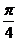 =
=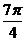
因此 =
=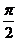 ,或
,或 =
=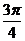


17.(本小题满分12分)
为拉动经济增长,某市决定新建一批重点工程,分别为基础设施工程、民生工程和产业建设工程三类,这三类工程所含项目的个数分别占总数的.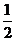 、
、 、
、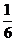 ,现在3名工人独立地从中任意一个项目参与建设要求:
,现在3名工人独立地从中任意一个项目参与建设要求:
(I)他们选择的项目所属类别互不相同的概率;

(II)至少有1人选择的项目属于民生工程的概率。
解:记第1名工人选择的项目属于基础设施工程、民生工程和产业建设工程分别为事件 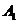 ,
,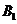 ,
,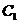 ,i=1,2,3.由题意知
,i=1,2,3.由题意知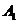
 相互独立,
相互独立,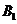
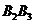 相互独立,
相互独立,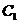
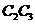 相互独立,
相互独立,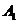 ,
,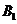 ,
,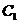 (i,j,k=1,2,3,且i,j,k互不相同)相互独立,
(i,j,k=1,2,3,且i,j,k互不相同)相互独立,
且P(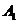 )=,p(
)=,p(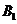 )=
)= ,p(
,p(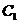 )=
)=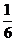


(1)他们选择的项目所属类别互不相同的概率
P=3!p(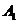

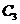 )=6p(
)=6p(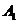 )p(
)p( )p(
)p(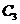 )
)
=6x 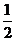 x
x x
x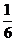 =
=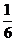
(1I)至少有1人选择的项目属于民生工程的概率
P=1-p(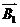

 )
)

=1-p(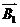 )p(
)p( )p(
)p( )
)
=1-(1-
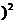 =
=