三、解答题：本大题共7小题，满分60分，解答时，请写出必要的演推过程。

19．（6分）（2013•滨州）（请在下列两个小题中，任选其一完成即可）

（1）解方程组：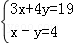

（2）解方程：．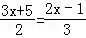

考点： 解二元一次方程组；解一元一次方程．

分析： （1）第二个方程两边乘以4加上第一个方程消去y求出x的值，进而求出y的值，即可确定出方程组的解；

（2）方程去分母后，去括号，移项合并，将x系数化为1，即可求出解．

解答： 解：（1），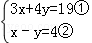

①+②×4得：7x=35，

解得：x=5，

将x=5代入②得：5﹣y=4，

解得：y=1，

则方程组的解为；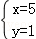

（2）去分母得：3（3x+5）=2（2x﹣1），

去括号得：9x+15=4x﹣2，

移项合并得：5x=﹣17，

解得：x=﹣．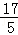

点评： 此题考查了解二元一次方程组，以及解一元一次方程，解方程组利用了消元的思想，消元的方法有：加减消元法与代入消元法．

20．（7分）（2013•滨州）（计算时不能使用计算器）

计算：．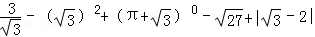

考点： 二次根式的混合运算；零指数幂；负整数指数幂．

专题： 计算题．

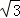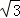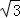分析： 根据零指数幂和负整数指数幂得原式=﹣3+1﹣3+2﹣，然后合并同类二次根式．

解答： 解：原式=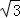﹣3+1﹣3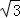+2﹣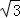

=﹣3．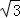

点评： 本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．也考查了零指数幂和负整数指数幂．

21．（8分）（2013•滨州）某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）．

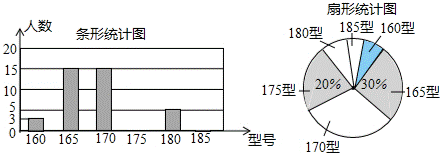
根据以上信息，解答下列问题：

（1）该班共有多少名学生？其中穿175型校服的学生有多少？

（2）在条形统计图中，请把空缺部分补充完整．

（3）在扇形统计图中，请计算185型校服所对应的扇形圆心角的大小；

（4）求该班学生所穿校服型号的众数和中位数．

考点： 条形统计图；扇形统计图；中位数；众数．

专题： 图表型．

分析： （1）根据穿165型的人数与所占的百分比列式进行计算即可求出学生总人数，再乘以175型所占的百分比计算即可得解；

（2）求出185型的人数，然后补全统计图即可；

（3）用185型所占的百分比乘以360°计算即可得解；

（4）根据众数的定义以及中位数的定义解答．

解答： 解：（1）15÷30%=50（名），50×20%=10（名），

即该班共有50名学生，其中穿175型校服的学生有10名；

（2）185型的学生人数为：50﹣3﹣15﹣15﹣10﹣5=50﹣48=2（名），

补全统计图如图所示；

（3）185型校服所对应的扇形圆心角为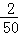：×360°=14.4°；

（4）165型和170型出现的次数最多，都是15次，

故众数是165和170；

共有50个数据，第25、26个数据都是170，

故中位数是170．

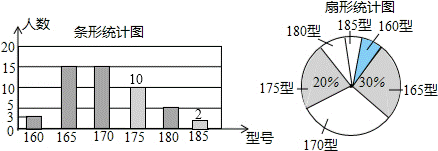
点评： 本题考查的是条形统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．除此之外，本题也考查了平均数、中位数、众数的认识．

22．（8分）（2013•滨州）如图，在△ABC中，AB=AC，点O在边AB上，⊙O过点B且分别与边AB、BC相交于点D、E，EF⊥AC，垂足为F．求证：直线EF是⊙O的切线．

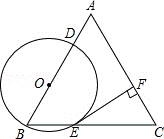
考点： 切线的判定．

专题： 证明题．

分析： 连接DE，则根据圆周角定理可得：DE⊥BC，由AB=AC，可得∠C=∠B，继而可得∠CEF+∠OEB=90°，由切线的判定定理即可得出结论．

解答： 解：连接DE，

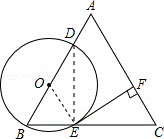
∵BD是⊙O的直径，

∴∠DEB=90°，

∵AB=AC，

∴∠ABC=∠C，

又∵OB=OE，

∴∠ABC=∠OEB，

∵∠FEC+∠C=90°，

∴∠FEC+∠OEB=90°，

∴OE⊥EF，

∵OE是⊙O半径，

∴直线EF是⊙O的切线．

点评： 本题考查了切线的判定、圆周角定理及等腰三角形的性质，关键是作出辅助线，利用等角代换得出∠OEF为直角，难度一般．

23．（9分）（2013•滨州）某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形．其中，抽屉底面周长为180cm，高为20cm．请通过计算说明，当底面的宽x为何值时，抽屉的体积y最大？最大为多少？（材质及其厚度等暂忽略不计）．

考点： 二次函数的应用．

分析： 根据题意列出二次函数关系式，然后利用二次函数的性质求最大值．

解答： 解：已知抽屉底面宽为x cm，则底面长为180÷2﹣x=（90﹣x）cm．

由题意得：y=x（90﹣x）×20

=﹣20（x2﹣90x）

=﹣20（x﹣45）2+40500

当x=45时，y有最大值，最大值为40500．

答：当抽屉底面宽为45cm时，抽屉的体积最大，最大体积为40500cm3．

点评： 本题考查利用二次函数解决实际问题．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法，常用的是后两种方法，当二次系数a的绝对值是较小的整数时，用配方法较好，如y=﹣x2﹣2x+5，y=3x2﹣6x+1等用配方法求解比较简单．

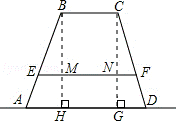
24．（10分）（2013•滨州）某高中学校为高一新生设计的学生板凳的正面视图如图所示，其中BA=CD，BC=20cm，BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm．为使板凳两腿底端A、D之间的距离为50cm，那么横梁EF应为多长？（材质及其厚度等暂忽略不计）．

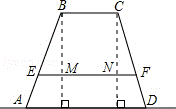
考点： 相似三角形的应用；等腰梯形的性质．

分析： 根据等腰梯形的性质，可得AH=DG，EM=NF，先求出AH、GD的长度，再由△BEM∽△BAH，可得出EM，继而得出EF的长度．

解答： 解：由题意得，MH=8cm，BH=40cm，则BM=32cm，

∵四边形ABCD是等腰梯形，AD=50cm，BC=20cm，

∴AH=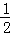（AD﹣BC）=15cm．

∵EF∥CD，

∵△BEM∽△BAH，

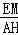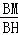∴=，即=，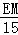

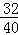解得：EM=12，

故EF=EM+NF+BC=2EM+BC=44cm．

答：横梁EF应为44cm．

点评： 本题考查了相似三角形的应用及等腰梯形的性质，解答本题的关键是熟练掌握等腰梯形的性质，这些是需要我们熟练记忆的内容．

25．（12分）（2013•滨州）根据要求，解答下列问题：

（1）已知直线l1的函数表达式为y=x，请直接写出过原点且与l1垂直的直线l2的函数表达式；

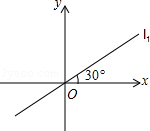
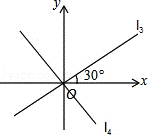
（2）如图，过原点的直线l3向上的方向与x轴的正方向所成的角为30°．

①求直线l3的函数表达式；

②把直线l3绕原点O按逆时针方向旋转90°得到的直线l4，求直线l4的函数表达式．

（3）分别观察（1）（2）中的两个函数表达式，请猜想：当两直线垂直时，它们的函数表达式中自变量的系数之间有何关系？请根据猜想结论直接写出过原点且与直线y=﹣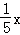垂直的直线l5的函数表达式．

考点： 一次函数综合题．

分析： （1）根据题意可直接得出l2的函数表达式；

（2）①先设直线l3的函数表达式为y=k1x（k1≠0），根据过原点的直线l3向上的方向与x轴的正方向所成的角为30°，直线过一、三象限，求出k1=tan30°，从而求出直线l3的函数表达式；

②根据l3与l4的夹角是为90°，求出l4与x轴的夹角是为60°，再设l4的解析式为y=k2x（k2≠0），根据直线l4过二、四象限，求出k2=﹣tan60°，从而求出直线l4的函数表达式；

（3）通过观察（1）（2）中的两个函数表达式可得出它们的函数表达式中自变量的系数互为负倒数关系，再根据这一关系即可求出与直线y=﹣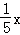垂直的直线l5的函数表达式．

解答： 解：（1）根据题意得：y=﹣x；

（2）①设直线l3的函数表达式为y=k1x（k1≠0），

∵过原点的直线l3向上的方向与x轴的正方向所成的角为30°，直线过一、三象限，

∴k1=tan30°=，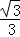

∴直线l3的函数表达式为y=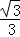x；

②∵l3与l4的夹角是为90°，

∴l4与x轴的夹角是为60°，

设l4的解析式为y=k2x（k2≠0），

∵直线l4过二、四象限，

∴k2=﹣tan60°=﹣，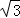

∴直线l4的函数表达式为y=﹣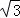x；

（3）通过观察（1）（2）中的两个函数表达式可知，当两直线互相垂直时，它们的函数表达式中自变量的系数互为负倒数关系，

∴过原点且与直线y=﹣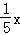垂直的直线l5的函数表达式为y=5x．

点评： 此题考查了一次函数的综合，用到的知识点是锐角三角函数、一次函数的解析式的求法，关键是根据锐角三角函数求出k的值，做综合性的题要与几何图形相结合，更直观一些．

点击此处下载文档(rar格式，228.69KB)