一、选择题(每小题3分,共30分)
1.(3分)(2013•鄂州)2013的相反数是( )
A. 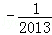 B.
B. 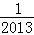 C. 3102 D. ﹣2013
C. 3102 D. ﹣2013
考点: 相反数.
分析: 直接根据相反数的定义求解.
解答: 解:2013的相反数为﹣2013.
故选D.
点评: 本题考查了相反数:a的相反数为﹣a.
2.(3分)(2013•鄂州)下列计算正确的是( )
A. a4•a3=a12 B. 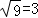 C. (x2+1)0=0 D. 若x2=x,则x=1
C. (x2+1)0=0 D. 若x2=x,则x=1
考点: 解一元二次方程-因式分解法;算术平方根;同底数幂的乘法;零指数幂.
分析: A、同底数的幂相乘,底数不变,指数相加;
B、通过开平方可以求得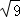 的值;
的值;
C、零指数幂:a0=1(a≠0);
D、先移项,然后通过提取公因式对等式的左边进行因式分解,然后解方程.
解答: 解:A、a4•a3=a(4+3)=a7.故本选项错误;
B、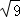 =
=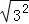 =|3|=3,故本选项正确;
=|3|=3,故本选项正确;
C、∵x2+1≠0,∴(x2+1)0=1.故本选项错误;
D、由题意知,x2﹣x=x(x﹣1)=0,则x=0或x=1.故本选项错误.
故选B.
点评: 本题综合考查了零指数幂、算术平方根、同底数幂的乘法以及解一元二次方程﹣﹣因式分解法.注意,任何不为零的数的零次幂等于1.
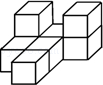
3.(3分)(2013•鄂州)如图,由几个相同的小正方体搭成的一个几何体,它的左视图为( )
A.  B.
B.  C.
C.  D.
D. 
考点: 简单组合体的三视图.
分析: 找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.
解答: 解:从左面看易得第一层有3个正方形,第二层最左边有一个正方形.
故选A.
点评: 本题考查了三视图的知识,左视图是从物体的左面看得到的视图.
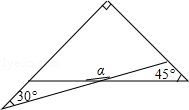
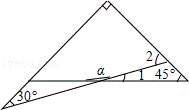
4.(3分)(2013•鄂州)一副三角板有两个直角三角形,如图叠放在一起,则∠α的度数是( )
A. 165° B. 120° C. 150° D. 135°
考点: 三角形的外角性质.
分析: 利用直角三角形的性质求得∠2=60°;则由三角形外角的性质知∠2=∠1+45°=60°,所以易求∠1=15°;然后由邻补角的性质来求∠α的度数.
解答: 解:如图,∵∠2=90°﹣30°=60°,
∴∠1=∠2﹣45°=15°,
∴∠α=180°﹣∠1=165°.
故选A.
点评: 本题考查了三角形的外角性质.解题时,注意利用题干中隐含的已知条件:∠1+α=180°.
5.(3分)(2013•鄂州)下列命题正确的个数是( )
①若代数式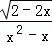 有意义,则x的取值范围为x≤1且x≠0.
有意义,则x的取值范围为x≤1且x≠0.
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元.
③若反比例函数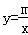 (m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
(m为常数),当x>0时,y随x增大而增大,则一次函数y=﹣2x+m的图象一定不经过第一象限.
④若函数的图象关于y轴对称,则函数称为偶函数,下列三个函数:y=3,y=2x+1,y=x2中偶函数的个数为2个.
A. 1 B. 2 C. 3 D. 4
考点: 命题与定理.
分析: 根据有关的定理和定义作出判断即可得到答案.
解答: 解:①若代数式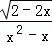 有意义,则x的取值范围为x<1且x≠0,原命题错误;
有意义,则x的取值范围为x<1且x≠0,原命题错误;
②我市生态旅游初步形成规模,2012年全年生态旅游收入为302 600 000元,保留三个有效数字用科学记数法表示为3.03×108元正确.
③若反比例函数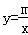 (m为常数)的增减性需要根据m的符号讨论,原命题错误;
(m为常数)的增减性需要根据m的符号讨论,原命题错误;
④若函数的图象关于y轴对称,则函数称为偶函数,三个函数中只有y=x2中偶函数,原命题错误,
故选C.
点评: 本题考查了命题与定理的知识,在判断 一个命题正误的时候可以举出反例.
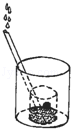
6.(3分)(2013•鄂州)一个大烧杯中装有一个小烧杯,在小烧杯中放入一个浮子(质量非常轻的空心小圆球)后再往小烧杯中注水,水流的速度恒定不变,小烧杯被注满后水溢出到大烧杯中,浮子始终保持在容器的正中间.用x表示注水时间,用y表示浮子的高度,则用来表示y与x之间关系的选项是( )
A. 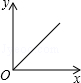 B.
B. 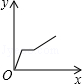 C.
C. 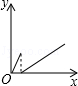 D.
D. 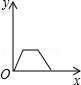
7.(3分)(2013•鄂州)如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD:CD=3:2,则tanB=( )
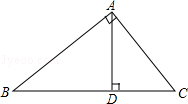
A. 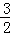 B.
B. 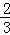 C.
C. 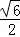 D.
D. 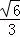
考点: 相似三角形的判定与性质;锐角三角函数的定义.
分析: 首先证明△ABD∽△ACD,然后根据BD:CD=3:2,设BD=3x,CD=2x,利用对应边成比例表示出AD的值,继而可得出tanB的值.
解答: 解:在Rt△ABC中,
∵AD⊥BC于点D,
∴∠ADB=∠CDA,
∵∠B+∠BAD=90°,∠BAD+DAC=90°,
∴∠B=∠DAC,
∴△ABD∽△ACD,
∴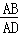 =
=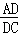 ,
,
∵BD:CD=3:2,
设BD=3x,CD=2x,
∴AD=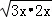 =
=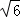 x,
x,
则tanB=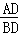 =
=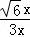 =
=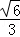 .
.
故选D.
点评: 本题考查了相似三角形的判定与性质及锐角三角函数的定义,难度一般,解答本题的关键是根据垂直证明三角形的相似,根据对应变成比例求边长.
8.(3分)(2013•鄂州)已知m,n是关于x的一元二次方程x2﹣3x+a=0的两个解,若(m﹣1)(n﹣1)=﹣6,则a的值为( )
A. ﹣10 B. 4 C. ﹣4 D. 10
考点: 根与系数的关系.
专题: 计算题.
分析: 利用根与系数的关系表示出m+n与mn,已知等式左边利用多项式乘多项式法则变形,将m+n与mn的值代入即可求出a的值.
解答: 解:根据题意得:m+n=3,mn=a,
∵(m﹣1)(n﹣1)=mn﹣(m+n)+1=﹣6,
∴a﹣3+1=﹣6,
解得:a=﹣4.
故选C
点评: 此题考查了根与系数的关系,熟练掌握根与系数的关系是解本题的关键.
9.(3分)(2013•鄂州)小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤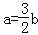 .
.
你认为其中正确信息的个数有( )
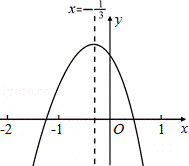
A. 2个 B. 3个 C. 4个 D. 5个
考点: 二次函数图象与系数的关系.
分析: 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答: 解:①如图,∵抛物线开口方向向下,∴a<0.
∵对称轴x=﹣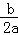 =﹣
=﹣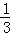 ,∴b=
,∴b=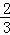 a<0,
a<0,
∴ab>0.故①正确;
②如图,当x=1时,y<0,即a+b+c<0.
故②正确;
③如图,当x=﹣1时,y=a﹣b+c>0,
∴2a﹣2b+2c>0,即3b﹣2b+2c>0,
∴b+2c>0.
故③正确;
④如图,当x=﹣1时,y>0,即a﹣b+c>0.
抛物线与y轴交于正半轴,则c>0.
∵b<0,
∴c﹣b>0,
∴(a﹣b+c)+(c﹣b)+2c>0,即a﹣2b+4c>0.
故④正确;
⑤如图,对称轴x=﹣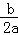 =﹣
=﹣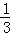 ,则
,则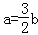 .故⑤正确.
.故⑤正确.
综上所述,正确的结论是①②③④⑤,共5个.
故选D.
点评: 本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
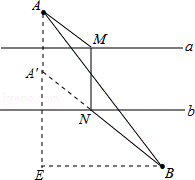
10.(3分)(2013•鄂州)如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=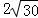 .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=( )
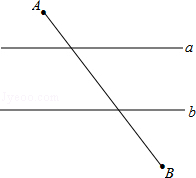
A. 6 B. 8 C. 10 D. 12
考点: 勾股定理的应用;线段的性质:两点之间线段最短;平行线之间的距离.
分析: MN表示直线a与直线b之间的距离,是定值,只要满足AM+NB的值最小即可,作点A关于直线a的对称点A′,连接A′B交直线b与点N,过点N作NM⊥直线a,连接AM,则可判断四边形AA′NM是平行四边形,得出AM=A′N,由两点之间线段最短,可得此时AM+NB的值最小.过点B作BE⊥AA′,交AA′于点E,在Rt△ABE中求出BE,在Rt△A′BE中求出A′B即可得出AM+NB.
解答: 解:作点A关于直线a的对称点A′,连接A′B交直线b与点N,过点N作NM⊥直线a,连接AM,
∵A到直线a的距离为2,a与b之间的距离为4,
∴AA′=MN=4,
∴四边形AA′NM是平行四边形,
∴AM+NB=A′N+NB=A′B,
过点B作BE⊥AA′,交AA′于点E,
易得AE=2+4+3=9,AB=2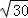 ,A′E=2+3=5,
,A′E=2+3=5,
在Rt△AEB中,BE=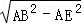 =
=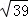 ,
,
在Rt△A′EB中,A′B=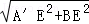 =8.
=8.
故选B.
点评: 本题考查了勾股定理的应用、平行线之间的距离,解答本题的关键是找到点M、点N的位置,难度较大,注意掌握两点之间线段最短.











