一、本大题共8小题,每小题5分,共40分。在每小题列出的四个选项中,选出符合题目要求的一项。
1.在复平面内,复数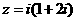 对应的点位于
对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知向量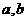 不共线,
不共线,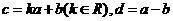 如果
如果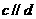 ,那么
,那么
A.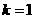 且
且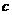 与
与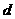 同向B.
同向B.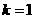 且
且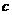 与
与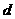 反向
反向
C.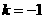 且
且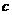 与
与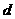 同向D.
同向D.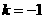 且
且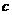 与
与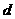 反向
反向
3.为了得到函数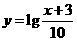 的图像,只需把函数
的图像,只需把函数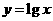 的图像上所有的点
的图像上所有的点
A.向左平移3个单位长度,再向上平移1个单位长度
B.向右平移3个单位长度,再向上平移1个单位长度
C.向左平移3个单位长度,再向下平移1个单位长度
D.向右平移3个单位长度,再向下平移1个单位长度
4.若正四棱柱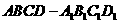 的底面边长为1,
的底面边长为1,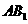 与底面
与底面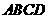 成60°角,则
成60°角,则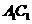 到底面
到底面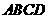 的距离为
的距离为
A.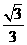 B.1 C.
B.1 C.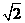 D.
D.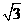
5.“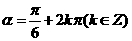 ”是“
”是“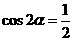 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
6.若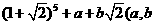 为有理数),则
为有理数),则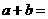
A.45 B.55 C.70D.80
7.用0到9这10个数字,可以组成没有重复数字的三位偶数的个数为
A.324 B.328 C.360D.648
8.点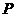 在直线
在直线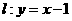 上,若存在过
上,若存在过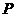 的直线交抛物线
的直线交抛物线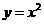 于
于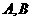 两点,且
两点,且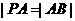 ,则称点
,则称点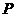 为“点”,那么下列结论中正确的是
为“点”,那么下列结论中正确的是
A.直线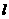 上的所有点都是“
上的所有点都是“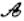 点”
点”
B.直线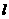 上仅有有限个点是“
上仅有有限个点是“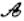 点”
点”
C.直线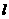 上的所有点都不是“
上的所有点都不是“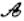 点”
点”
D.直线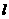 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“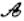 点”
点”
第Ⅱ卷(共110分)
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
9.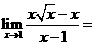 ___________。
___________。
10.若实数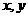 满足
满足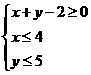 则
则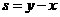 的最小值为__________。
的最小值为__________。
11.设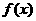 是偶函数,若曲线
是偶函数,若曲线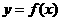 在点
在点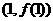 处的切线的斜率为1,则该曲线在点
处的切线的斜率为1,则该曲线在点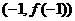 处的切线的斜率为______________。
处的切线的斜率为______________。
12.椭圆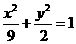 的焦点为
的焦点为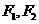 ,点
,点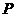 在椭圆上,若
在椭圆上,若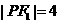 ,则
,则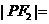 _________;
_________;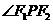 的小大为____________。
的小大为____________。
13.若函数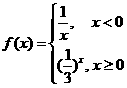 则不等式
则不等式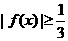 的解集为____________。
的解集为____________。
14.已知数列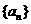 满足:
满足: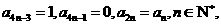 则
则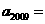 ________;
________;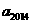 =____________。
=____________。
三 、解答题:本大题共6小题,共80分。解答应写出文字说明,演算步骤或证明过程。
15.(本小题共13分)
在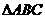 中,角
中,角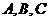 的对边分别为
的对边分别为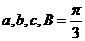 ,
,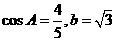 。
。
(I)求 的值;
的值;
(Ⅱ)求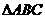 的面积。
的面积。
16.(本小题共14分)
如图,在三棱锥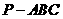 中,
中,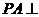 底面
底面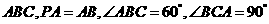 ,点
,点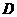 ,
,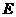 分别在棱
分别在棱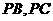 上,且
上,且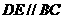
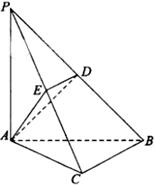
(I)求证: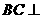 平面
平面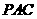 ;
;
(Ⅱ)当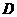 为
为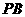 的中点时,求
的中点时,求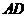 与平面
与平面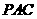 所成的角的大小;
所成的角的大小;
(Ⅲ)是否存在点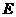 使得二面角
使得二面角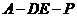 为直二面角?并说明理由。
为直二面角?并说明理由。
17.(本小题共13分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是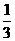 ,遇到红灯时停留的时间都是2min。
,遇到红灯时停留的时间都是2min。
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率; 

(Ⅱ)求这名学生在上学路上因遇到红灯停留的总时间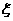 的分布列及期望。
的分布列及期望。
18.(本小题共13分)
设函数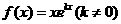
(I)求曲线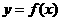 在点
在点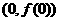 处的切线方程;
处的切线方程;
(Ⅱ)求函数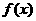 的单调区间;
的单调区间;
(Ⅲ)若函数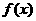 在区间
在区间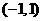 内单调递增,求
内单调递增,求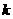 的取值范围。
的取值范围。
19.(本小题共14分)
已知双曲线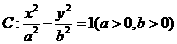 的离心率为
的离心率为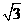 ,右准线方程为
,右准线方程为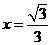
(I)求双曲线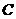 的方程;
的方程;
(Ⅱ)设直线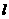 是圆
是圆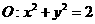 上动点
上动点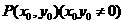 处的切线,
处的切线,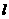 与双曲线
与双曲线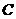 交于不同的两点
交于不同的两点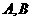 ,证明
,证明 的大小为定值。
的大小为定值。
20.(本小题共13分)
已知数集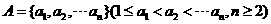 具有性质
具有性质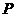 ;对任意的
;对任意的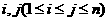 ,
,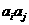 与
与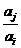 两数中至少有一个属于
两数中至少有一个属于 。
。
(I)分别判断数集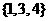 与
与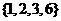 是否具有性质
是否具有性质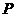 ,并说明理由;
,并说明理由;
(Ⅱ)证明: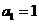 ,且
,且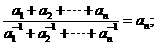
(Ⅲ)证明:当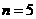 时,
时,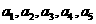 成等比数列。
成等比数列。











