第I卷(选择,共36分)
一、选择题(本大共12个小,每小3分,共36分)
在每小题给出的四个选项中,有且仅有一项是符合题目要求的.
1 一5的绝对值是
A. 5B.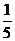 C. -
C. -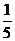 D. -5
D. -5
答案:A
解析:-5的绝对值是它的相反数,所以,选A。
2.已知空气的单位体积质量为1.24×10-3克/厘米3,将1.24×10-3用小数表示为
A: 0. 000124 B.0.0124 C.一0.00124 D、0.00124
答案:D
解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数。
1.24×10-3=0.00124
3、如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是

答案:C
解析:长方体的三视图为矩形,只有二个视图一样,圆柱的正视图与侧视图为矩形,俯视图为圆,三棱柱的正、侧视图为矩形,俯视图为三角形,只有球的三个视图都是圆。
4.下列计算正确的是

答案:B
解析: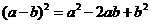 ,
,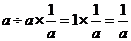 ,
,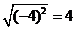 ,所以,A、C、D都错,只是B的计算是正确的。
,所以,A、C、D都错,只是B的计算是正确的。
5.如图.圆O的直径CD过弦EF的中点G, ∠DCF=20°.,则∠EOD等于
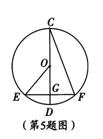
A. 10° B. 20° C. 40° D. 80°
答案:C
解析:因为直径过弦EF的中点G,所以,CD⊥EF,且平分弧EF,因此,弧ED与弧BD的度数都为40°,所以,∠EOD=40°,选C。
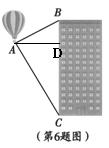
6.如图,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为300,看这栋高楼底部C的俯角为600,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为
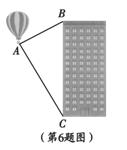 A. 40
A. 40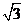 m B. 80
m B. 80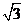 m
m
C. 120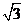 m D. 160
m D. 160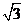 m
m
答案:D
解析:过A作AD⊥BC于D,则∠BAD=30°,∠CAD=60°,AD=120。
BC=BD+CD=120tan30°+120tan60°=160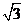 ,选D。
,选D。
7,某校八年级二班的10名团员在“情系芦山”的献爱心捐款活动中,捐款清况如下(单位:元):10, 8,12, 15,10,12,11,9,13,10,则这组数据的
A、众数是10.5 B.方差是3.8 C.极差是8 D,中位数是10
答案:B
解析:从数据可以看出,众数为10,极差为:15-8=7,中位数为:10.5,故A、C、D都错,由方差的计算公式可求得方差为3.8,选B。
8.适合不等式组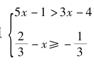 的全部整数解的和是
的全部整数解的和是
A.一1 B、0 C.1 D.2
答案:B
解析:解(1)得: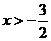 ,解(2)得:
,解(2)得: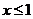 ,所以,原不等式组的解为:
,所以,原不等式组的解为: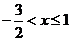 ,所有整数为:-1,0,1,和为0,故选B。
,所有整数为:-1,0,1,和为0,故选B。
9.如果三角形的两边分别为3和5,那么连结这个三角形三边中点所得的三角形的周长可能是
A. 5. 5 B、5 C.4.5 D.4
答案:A
解析:设第三边长为x,则2<x<8,三角形的周长设为p,则10<p<16,连结三边中点所得三角形的周长范围应在5到8之间,只有A符合。
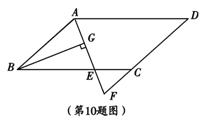
10.如图.在 ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,若BG=4
ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,若BG=4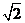 ,则△CEF的面积是
,则△CEF的面积是
A、2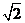 B、
B、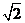 C、3
C、3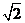 D、4
D、4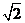
答案:A
解析:∵在▱ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,∵AB∥DF,∠BAF=∠F,∴∠F=∠DAF,
∴△ADF是等腰三角形,AD=DF=9;∵AB=CD=6, ∴CF=3;
∠BEA=∠DAF=∠BAF,所以,BA=BE,
∴在△ABG中,BG⊥AE,AB=6,BG=4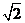 可得:AG=2,
可得:AG=2,
又∵BG⊥AE,∴AE=2AG=4,∴△ABE的面积等于8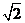 ,
,
又∵▱ABCD,∴△CEF∽△BEA,相似比为1:2,面积1:4,∴△CEF的面积为,2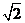 .
.
∴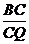 =
=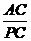 ,AC、BC为定值,所以PC最大时,CQ取到最大值.
,AC、BC为定值,所以PC最大时,CQ取到最大值.
∵AB=5,tan∠ABC=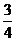 ,即BC:CA=4:3,所以,∴BC=4,AC=3.
,即BC:CA=4:3,所以,∴BC=4,AC=3.
PC的最大值为直线5,所以,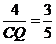 ,所以,CQ的最大值为
,所以,CQ的最大值为