一、选择题(本大题共7小题,每小题3分,共21分)
1.(3分)(2014年福建厦门)sin30°的值是( )
A.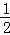 B.
B.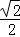 C.
C.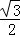 D. 1
D. 1
分析: 直接根据特殊角的三角函数值进行计算即可.
解答: 解:sin30°=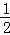 .
.
故选A.
点评: 本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.
2.(3分)(2014年福建厦门)4的算术平方根是( )
A. 16 B. 2 C. ﹣2 D. ±2
考点: 算术平方根.
分析: 根据算术平方根定义求出即可.
解答: 解:4的算术平方根是2,
故选B.
点评: 本题考查了对算术平方根的定义的应用,主要考查学生的计算能力.
3.(3分)(2014年福建厦门)3x2可以表示为( )
A. 9x B. x2•x2•x2 C. 3x•3x D. x2+x2+x2
考点: 单项式乘单项式;合并同类项;同底数幂的乘法.
专题: 计算题.
分析: 各项计算得到结果,即可做出判断.
解答: 解:3x2可以表示为x2+x2+x2,
故选D
点评: 此题考查了单项式乘以单项式,合并同类项,以及同底数幂的乘法,熟练掌握运算法则是解本题的关键.
4.(3分)(2014年福建厦门)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A.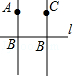 B.
B.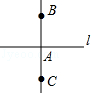 C.
C.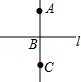 D.
D.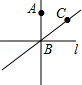
考点: 垂线.
分析: 根据题意画出图形即可.
解答: 解:根据题意可得图形 ,
,
故选:C.
点评: 此题主要考查了垂线,关键是掌握垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
5.(3分)(2014年福建厦门)已知命题A:任何偶数都是8的整数倍.在下列选项中,可以作为“命题A是假命题”的反例的是( )
A. 2k B. 15 C. 24 D. 42
考点: 命题与定理.
分析: 证明命题为假命题,通常用反例说明,此反例满足命题的题设,但不满足命题的结论.
解答: 解:42是偶数,但42不是8的倍数.
故选D.
点评: 本题考查了命题:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式;有些命题的正确性是用推理证实的,这样的真命题叫做定理.
6.(3分)(2014年福建厦门)如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
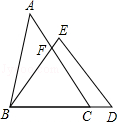
A. ∠EDB B. ∠BED C.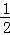 ∠AFB D. 2∠ABF
∠AFB D. 2∠ABF
考点: 全等三角形的判定与性质.
分析: 根据全等三角形的判定与性质,可得∠ACB与∠DBE的关系,根据三角形外角的性质,可得答案.
解答: 解:在△ABC和△DEB中,
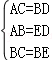 ,
,
∴△ABC≌△DEB (SSS),
∴∠ACB=∠DEB.
∵∠AFB是△BCF的外角,
∴∠ACB+∠DBE=∠AFB,
∠ACB=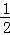 ∠AFB,
∠AFB,
故选:C.
点评: 本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,三角形外角的性质.
7.(3分)(2014年福建厦门)已知某校女子田径队23人年龄的平均数和中位数都是13岁,但是后来发现其中一位同学的年龄登记错误,将14岁写成15岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A. a<13,b=13 B. a<13,b<13 C. a>13,b<13 D. a>13, b=13
b=13
考点: 中位数;算术平均数.
分析: 根据平均数的计算公式求出正确的平均数,再与原来的平均数进行比较,得出a的值,根据中位数的定义得出最中间的数还是13岁,从而选出正确答案.
解答: 解:∵原来的平 均数是13岁,
均数是13岁,
∴13×23=299(岁),
∴ 正确的平均数a=
正确的平均数a=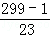 ≈12.97<13,
≈12.97<13,
∵原来的中位数13岁,将14岁写成15岁,最中间的数还是13岁,
∴b= 13;
13;
故选D.
点评: 此题考查了中位数和平均数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
二、填空题(本大题共1 0小题,每小题4分,共40分)
0小题,每小题4分,共40分)
8.(4分)(2014年福建厦门)一个圆形转盘被平均分成红、黄、蓝、白4个扇形区域,向其投掷一枚飞镖,飞镖落在转盘上,则落在黄色区域的概率是 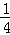 .
.
考点: 几何概率.
分析: 根据概率公式,求出红色区域的面积与总面积的比即可解答.
解答: 解:∵圆形转盘平均分成红、黄、蓝、白4个扇形区域,其中黄色区域占1份,
∴飞镖落在黄色区域的概率是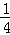 ;
;
故答案为: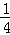 .
.
点评: 本题考查了几何概率的运用,用到的知识点是概率公式,在解答时根据概率=相应的面积与总面积之比是解答此类问题关键.
9.(4分)(2014年福建厦门)若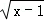 在实数范围内有意义,则x的取值范围是 x≥1 .
在实数范围内有意义,则x的取值范围是 x≥1 .
考点: 二次根式有意义的条件.
分析: 先根据二次根式有意义的条件列出关于x的不等式,求出x的取值 范围即可.
范围即可.
解答: 解:∵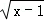 在实数范围内有意义,
在实数范围内有意义,
∴x﹣1≥0,
解得x≥1.
故答案为:x≥1.
点评: 本题考查的是二次根式有意义的条件,即被开方数大于等于0.
10.(4分)(2014年福建厦门)四边形的内角和是 360 °.
考点: 多边形内角与外角.
专题: 计算题.
分析: 根据n边形的内角和是(n﹣2)•180°,代入公式就可以求出内角和.
解答: 解:(4﹣2)•180°=360°.
故答案为360°.
点评: 本题主要考查了多边形的内角和公式,是需要识记的内容,比较简单.
11.(4分)(2014年福建厦门)在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA向右平移3个单位,得到线段O1A1,则点O1的坐标是 (3,0) ,A1的坐标是 (4,3) .
考点: 坐标与图形变化-平移.
分析: 根据向右平移,横坐标加,纵坐标不变解答.
解答: 解:∵点O(0,0),A(1,3),线段OA向右平移3个单位,
∴点O1的坐标是(3,0),A1的坐标是(4,3).
故答案为:(3,0),(4,3).
点评: 本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
12.(4分)(2014年福建厦门)已知一组数据:6,6,6,6,6,6,则这组数据的方差为 0 .
【注:计算方差的公式是S2=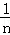 [(x1﹣
[(x1﹣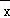 )2+(x2﹣
)2+(x2﹣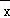 )2+…+(xn﹣
)2+…+(xn﹣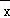 )2]】
)2]】
考点: 方差.
分析: 根据题意得出这组数据的平均数是6,再根据方差S2=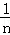 [(x1﹣
[(x1﹣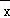 )2+(x2﹣
)2+(x2﹣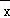 )2+…+(xn﹣
)2+…+(xn﹣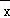 )2],列式计算即可.
)2],列式计算即可.
解答: 解:∵这组数据的平均数是6,
∴这组数据的方差=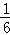 [6×(6﹣6)2]=0.
[6×(6﹣6)2]=0.
故答案为:0.
点评: 本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为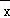 ,则方差S2=
,则方差S2=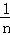 [(x1﹣
[(x1﹣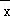 )2+(x2﹣
)2+(x2﹣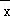 )2+…+(xn﹣
)2+…+(xn﹣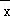 )2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
13.(4分)(2014年福建厦门)方程x+5=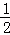 (x+3)的解是 x=﹣7 .
(x+3)的解是 x=﹣7 .
考点: 解一元一次方程.
专题: 计算题.
分析: 方程去分母,移项合并,将x系数化为1,即可求出解.
解答: 解:去分母得:2x+10=x+3,
解得:x=﹣7.
故答案为:x=﹣7
点评: 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,将未知数系数化为1,即可求出解.
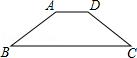
14.(4分)(2014年福建厦门)如图,在等腰梯形ABCD中,AD∥BC,若AD=2,BC=8,梯形的高是3,则∠B的度数是 45° .
考点: 等腰梯形的性质.
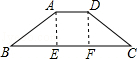
分析: 首先过点A作AE⊥BC交BC于E,过点D作DF⊥BC交BC于F,易得四边形AEFD是长方形,易证得△ABE是等腰直角三角形,即可得∠B的度数.
解答: 解:过点A作AE⊥BC交BC于E,过点D作DF⊥BC交BC于F,
∵AD∥BC,
∴四边形AEFD是长方形,
∴EF=AD=2,
∵四边形ABCD是等腰梯形,
∴BE=(8﹣2)÷2=3,
∵梯形的高是3,
∴△ABE是等腰直角三角形,
∴∠B=45°.
故答案为:45°.
点评: 此题考查了等腰梯形的性质以及等腰直角三角形的判定与性质.此题注意掌握辅助线的作法,注意掌握数形结合思想的应用.
15.(4分)(2014年福建厦门)设a=192×918,b=8882﹣302,c=10532﹣7472,则数a,b,c按从小到大的顺序排列,结果是 a < c < b .
考点: 因式分解的应用.
分析: 运用平方差公式进行变形,把其中一个因数化为918,再比较另一个因数,另一个因数大的这个数就大.
解答: 解:a=192×918=361×918,
b=8882﹣302=(888﹣30)(888+30)=858×918,
c=10532﹣7472=(1053+747)(1053﹣747)=1800×306=600×918,
所以a<c<b.
故答案为:a<c<b.
点评: 本题主要考查了因式分解的应用,解题的关键是运用平方差公式进行化简得出一个因数为918.
16.(4分)(2014年福建厦门)某工厂一台机器的工作效率相当于一个工人工作效率的12倍,用这台机器生产60个零件比8个工人生产这些零件少用2小时,则这台机器每小时生产 15 个零件.
考点: 分式方程的应用.
分析: 设一个工人每小时生产零件x个,则机器一个小时生产零件12x个,根据这台机器生产60个零件比8个工人生产这些零件少用2小时,列方程求解,继而可求得机器每小时生产的零件.
解答: 解:设一个工人每小时生产零件x个,则机器一个小时生产零件12x 个,
个,
由题意得,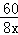 ﹣
﹣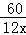 =2,
=2,
解得:x=1.25,
经检验:x=1.25是原分式方程的解,且符合题意,
则12x=12×1.25=15.
即这台机器每小时生产15个零件.
故答案为:15.
点评: 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.
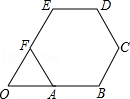
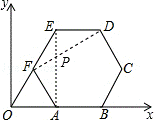
17.(4分)(2014年福建厦门)如图,正六边形ABCDEF的边长为2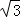 ,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是( 2
,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线AE的交点坐标是( 2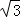 , 4 ).
, 4 ).
考点: 正多边形和圆;两条直线相交或平行问题.
分析: 首先得出△AOF是等边三角形,利用建立的坐标系,得出D,F点坐标,进而求出直线DF的解析式,进而求出横坐标为2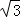 时,其纵坐标即可得出答案.
时,其纵坐标即可得出答案.
解答: 解:连接AE,DF,
∵正六边形ABCDEF的边长为2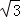 ,延长BA,EF交于点O,
,延长BA,EF交于点O,
∴可得:△AOF是等边三角形,则AO=FO=FA=2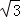 ,
,
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=4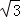 ,
,
∴∠EAO=90°,∠OEA=30°,故AE=4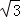 cos30°=6,
cos30°=6,
∴F(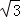 ,3),D(4
,3),D(4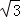 ,6),
,6),
设直线DF的解析式为:y=kx+b,
则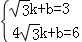 ,
,
解得: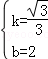 ,
,
故直线DF的解析式为:y=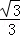 x+2,
x+2,
当x=2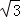 时,y=2
时,y=2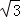 ×
×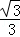 +2=4,
+2=4,
∴直线DF与直线AE的交点坐标是:(2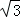 ,4).
,4).
故答案为:2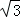 ,4.
,4.
点评: 此题主要考查了正多边形和圆以及待定系数法求一次函数解析式等知识,得出F,D点坐标是解题关键.











