一、选择题(本大题共有8小 题,每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的)。
1.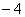 的绝对值是
的绝对值是
A.4 B.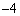 C.
C.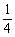 D.
D.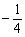
2.下列立体图形中,侧面展开图是扇形的是

3.下面的图形中,既是轴对称图形又是中心对称图形的是
A.  B.
B.  C.
C.  D.
D. 
4.下列运算正确的是
A.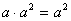 B.
B.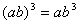 C.
C.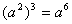 D.
D.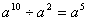
5.如图,⊙O的直径CD⊥AB,∠AOC=50°,则∠CDB大小为
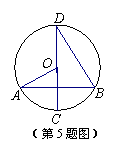
A.25° B.30° C.40° D.50°
6.下列说法中正确的是
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的概率为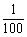 ,说明每买100张奖券,一定有一次中奖;
,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解 盐城市城镇居民人均年收入水平,宜采用抽样调查.
盐城市城镇居民人均年收入水平,宜采用抽样调查.
7. 若直线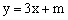 经过第一、三、四象限,则抛物线
经过第一、三、四象限,则抛物线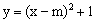 的顶点必在
的顶点必在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
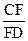
 8.如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A’、D’处,且A’D’经过B,EF为折痕,当D’F⊥CD时, 的值为
8.如图,菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在A’、D’处,且A’D’经过B,EF为折痕,当D’F⊥CD时, 的值为
A. 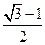 B.
B. 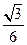 C.
C. 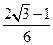 D.
D. 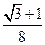
二、填空题(本大题共有10小题,每小题3分, 共30分.不需写出解答过程,)
共30分.不需写出解答过程,)
9.点A(﹣3,0)关于y轴的对称点的坐标是 .
10.函数y=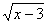 中自变量x的取值范围是_________,
中自变量x的取值范围是_________,
11.因式分解:a2+2a+1= .
12. PM 2.5是指大气中直径小于或等于0.0000025 m的颗粒物,将0.0000025用科学记数法表示为_________,
13.已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为________cm2.
14.如图是甲、乙两射击运动员的10次射击训练成绩(环数)的折线统计图,观察图形,甲、乙这10次射击成绩的方差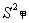 ,
,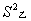 之间的大小关系是 .
之间的大小关系是 .
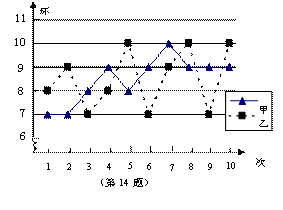 15.已知
15.已知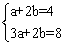 ,则a+b等于
,则a+b等于
16.某种商品原价是120元,经两次降价后的价格是100元,求平均每次降价的百分率.设平均每次降价的百分率为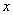 ,可列方程为 .
,可列方程为 .
17.已知⊙O1与⊙O2的半径分别是方程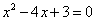 的两根,且
的两根,且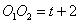 ,若这两个圆相切,则
,若这两个圆相切,则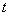 = .
= .
18.任何实数a,可用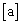 表示不超过a的最大整数,如
表示不超过a的最大整数,如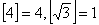 ,现对72进行如下操作:
,现对72进行如下操作: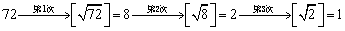 ,这样对72只需进行3次操作后变为1,那么只需进行3次操作后变为1的所有正整数中,最大的是 .
,这样对72只需进行3次操作后变为1,那么只需进行3次操作后变为1的所有正整数中,最大的是 .
三、解答题(本大题共有10小题,共96分解答时应写出文字说明、推理过程或演算步骤)
19.(本题满分8分)
(1)计算: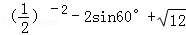 ; (2)解方程: - = 2.
; (2)解方程: - = 2.
20.(本题满分8分)解不等式组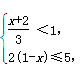 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.
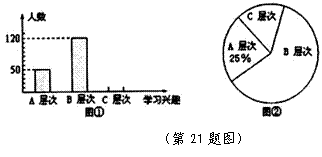
21.(本题满分8分) 学生的学习兴趣如何是每位教师非常关注的问题.为此,某校教师对该校部分学生的学习兴趣进行了一次抽 样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣),并将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣),并将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
⑴ 此次抽样调查中,共调查了 名学生;
⑵ 将图①、图②补充完整;
⑶ 求图②中C层次所在扇形的圆心角的度数;
⑷ 根据抽样调查结果,请你估算该校1200名学生中大约有多少名学生对学习感兴趣(包括A层次和B层次).
22.(本题满分8分)
一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ▲ ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数 的概率.(请用“画树状图”或“列表”的方法写出过程)
的概率.(请用“画树状图”或“列表”的方法写出过程)
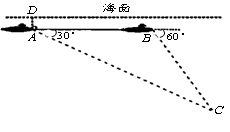
23.(本题满分8分)如图,一艘核潜艇在海面下500米A点处测得俯角为30°正前方的海底有黑匣子信号发出,继续在同一深度直线航行3000米后再次在B点处测得俯角为60°正前方的海底有黑匣子信号发出,求海底黑匣子C点处距离海面的深度?(保留根号)