1. 设 ,
, ,
,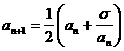 ,
,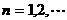 ,证明:数列
,证明:数列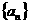 收敛,并求其极限。(12分)
收敛,并求其极限。(12分)
2. 设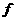 在
在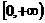 上连续,满足
上连续,满足 ,
, ,设
,设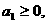
 ,
,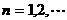 ,证明:(1)
,证明:(1)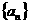 为收敛数列;(2)设
为收敛数列;(2)设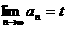 ,则有
,则有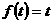 ;(3)若条件改为
;(3)若条件改为 ,
,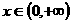 ,则
,则 。(14分)
。(14分)
3. 设 ,
, 在原点的某邻域内连续,且
在原点的某邻域内连续,且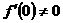 。证明
。证明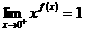 。(10分)
。(10分)
4. 证明:若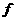 在
在 上连续增,
上连续增, ,则
,则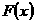 为
为 上的单调增函数。(10分)
上的单调增函数。(10分)
5. 设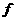 为
为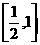 上连续函数,证明:(1)
上连续函数,证明:(1) 在
在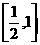 上收敛;(2)
上收敛;(2) 在
在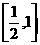 上一致收敛的充要条件是
上一致收敛的充要条件是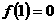 。(12分)
。(12分)
6. 设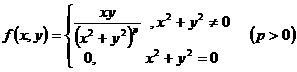 ,试讨论函数在
,试讨论函数在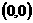 处的连续性。(10分)
处的连续性。(10分)
7. 计算曲线积分: ,其中
,其中 为常数,
为常数,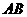 为由
为由 到
到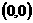 经过圆
经过圆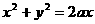 上半部的路线。(14分)
上半部的路线。(14分)
8. 设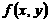 在
在 上连续,且恒取正值,求:
上连续,且恒取正值,求: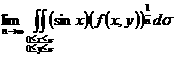 。
。
(12分)
9. 设周期为 的可积函数
的可积函数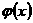 与
与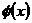 满足关系式:
满足关系式: ,则给出函数
,则给出函数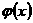 的 Fourier系数
的 Fourier系数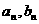 与函数
与函数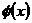 的 Fourier系数
的 Fourier系数 之间的关系。(14分)
之间的关系。(14分)
10. 设函数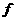 定义在
定义在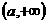 上,
上,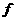 在每一个有限区间
在每一个有限区间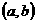 内有界,并满足
内有界,并满足 ,证明:
,证明: 。(8分)
。(8分)
11. 设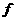 在
在 上连续,又有
上连续,又有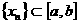 ,使
,使  ,证明:存在
,证明:存在 ,使得
,使得 。(10分)
。(10分)
12. 设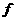 为区间
为区间 上的单调有界函数,证明:若
上的单调有界函数,证明:若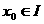 为
为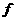 的间断点,则
的间断点,则 必是
必是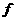 的第一类间断点。(8分)
的第一类间断点。(8分)
13. 已知函数 在区间
在区间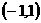 内有二阶导数,且
内有二阶导数,且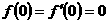 ,
, ,求证:
,求证: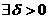 ,使得
,使得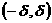 内
内 。(8分)
。(8分)
14. 设级数 收敛,
收敛,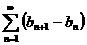 绝对收敛,试征:级数
绝对收敛,试征:级数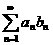 也收敛。(8分)
也收敛。(8分)











