第Ⅰ卷 选择题 (共40分)
一、选择题(共10个小题,每小题4分,共40分)
1、比-1大1的数是 ( )
A.2 B.1 C .0 D.-2
.0 D.-2
2.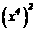 等于 ( )
等于 ( )
A.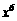 B.
B.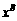 C.
C.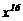 D.
D.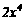
3.如图,是由几个小立方体所搭成的几何体的俯视图,小正 方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是 ( )
方形中的数字表示在该位置上的立方体的个数,这个几何体的正视图是 ( )
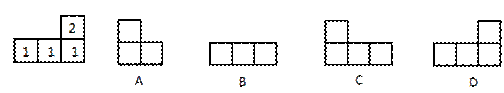
4.拒绝“餐桌浪 费”刻不容缓,据统计
费”刻不容缓,据统计 全国每年浪费食物总量约为50000000000千克,这个数据用科学记数法表示为 ( )
全国每年浪费食物总量约为50000000000千克,这个数据用科学记数法表示为 ( )
A.5×1010 B.0.5×1011 C.5×1011 D.0.5×1010
5.一元二次方程x2-4x+5=0的根的情况是 ( )
A.有两个不相等的实数根B.有两个相等的实数根C.只有一个实数根D.没有实数 根.
根.
6.下面的图形中,既是轴对称图形又是中心对称图形的是 ( )
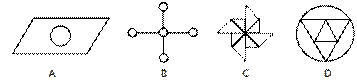
7.一组数据,6、4、a、3、2的平均数是5,这组数据的方差为 ( )
A.8 B.5 C.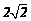 D.3
D.3
8 .一个扇形的半径为8cm,弧长为
.一个扇形的半径为8cm,弧长为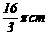 ,则扇形的圆心角为 ( )
,则扇形的圆心角为 ( )
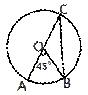
A.60° B.120° C.150° D.180°
9.关于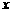 的函数
的函数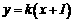 和
和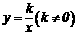 在同一坐标系中的图像大致是( )
在同一坐标系中的图像大致是( )
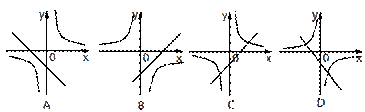
10.如图,在半径为1的⊙O中,∠AOB=45°,则sinC的值为( )
A.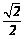 B.
B.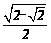 C.
C.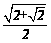 D.
D.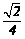
第Ⅱ卷 非选择题( 共110分)
二、填空题(共5个小题,每小题4分,共20分)
11.因式分解:x2y-y=___________ .
12.不等式组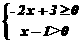 的解集是__________.
的解集是__________.
13.一个多边形的内角和比它的外角和的3倍少180°,则它的边数是__________.
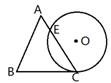
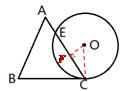
14.如图,一个边长为4cm的等边三角形ABC的高与⊙O的直径相等.⊙O与BC相切于点C与AC相交于点E。则CE的长为 __________cm.
15.一次函数y=kx+b,当1≤x≤4时,3≤y≤6,则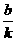 的值是__________.
的值是__________.
三、解答题(共2个题,每题8分,共16分)
16.解方程: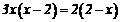
17.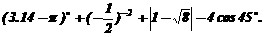
四、解答题(共2个题,每小题8分,共16分)
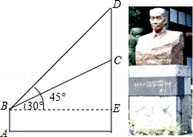
18.如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A处自B点看雕塑头顶D的仰角为450,看雕塑底部C的 仰角为300,求塑像CD的高度。(最后结果精确到0.1米,参考数据:
仰角为300,求塑像CD的高度。(最后结果精确到0.1米,参考数据: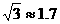 )
)

19.如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G..
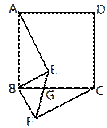
⑴.求证:AE=CF
⑵.若∠ABE=55°,求∠EGC的大小。
五、解答题(共2个题,每题10分,共20分)
20.为了提高学生书写汉字的能力, 增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经
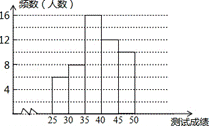
增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经 选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
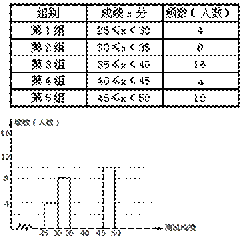
请结合图表完成下列各题:
⑴.求表中a的值;
⑵.请把频数分布直方图补充完整;
⑶.若测试成绩不低于40分为优秀,则本次测试 的优秀率是多
的优秀率是多 少?
少?
⑷.第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小宇与小强两名男同学能分在同一组的概率.
21、学校新到 一批理
一批理 、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务。
、化、生实验器材需要整理,若实验管理员李老师一人单独整理需要40分钟完成,现在李老师与工人王师傅共同整理20分钟后,李老师因事外出,王师傅再单独整理了20分钟才完成任务。
⑴.王师傅单独整理这批实验器材需要多少分钟?
⑵.学校要求王师傅的工作时间不能超过30分钟,要完成整理这批器材,李老师至少要工作多少分钟?
六、解答题(本题满分12分)
22.如图,一次函数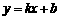 与反比例函数
与反比例函数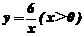 的图像交于A(m,6),B
的图像交于A(m,6),B (3,n)两点。
(3,n)两点。

⑴.求一次函数的解析式;
⑵.根据图像直接写出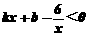 的x的取值范围;
的x的取值范围;
 ⑶.求△AOB的面积。
⑶.求△AOB的面积。
七、解答题(本题满分12分)
23. 阅读理解:
如图①,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”。
解决问题:
⑴.如图①,∠A=∠B=∠DEC =45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
⑵.如图②,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试 在图②中画出矩形ABCD的边AB上的强相似点;
在图②中画出矩形ABCD的边AB上的强相似点;
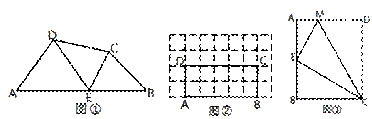
⑶.如图③,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系。
八、解答题(本题满分14分)
24.如图,已知抛物线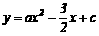 与
与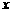 轴相交于A、B两点,并与直线
轴相交于A、B两点,并与直线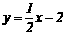 交于B、C两点,其中点C是直线
交于B、C两点,其中点C是直线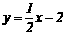 与
与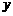 轴的交点,连接AC。
轴的交点,连接AC。
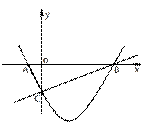
⑴.求抛物线的解析式;
⑵.证明:△ABC为直角三角形;
⑶.△ABC内部能否截出面积最大的矩形DEFG?(顶点D、E、F、G在△ABC各边上)若能,求出最大面积;若不能,请说明理由。(答题卡上的备用图①、②供解题时选用)
四川省自贡市2014年初中毕业生学业考试 数学试卷参考答案
一、选择题选择题(共10个小题,每小题4分,共40分)
题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答 案 | C | B | D | A | D | C | A | B | D | B |
10题略解:过点 作
作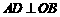 于点D.
于点D.

∵在 中,
中,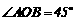
∴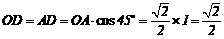
 ∴
∴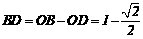
∴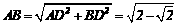
∵AC是⊙O的直径,
∴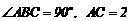
∴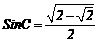 故选B
故选B
二、填空题(共5个小题,每小题4分,共20分)
11. 分解因式: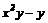 =
=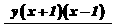 .
.
12. 解集是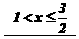 .
.
13. 它的边数是 9 .
14. CE的长为 3 cm.
分析:作如图所示的辅助线.根据△ABC为等边三角形,且边长为4,易求故高为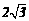 ,即
,即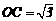 ;又
;又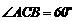 ,故有
,故有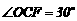 ;在
;在
 ,可得
,可得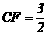 ,即
,即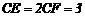 .
.
15. 2或﹣7. 分析:由于k的符号不能确定,故应分k>0和k<0两种进行解答.
三、解答题(共2个题,每题8分,共16分)
16.(8分)解方程: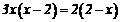
略解: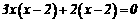

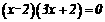
所以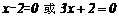 解得:
解得:
17.(8分)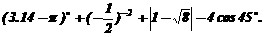
略解:原式=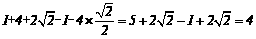
四、解答题(共2个题,每小题8分,共16分)
18.(8分)略解:
在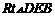 中,
中, 米;
米;
在 中,
中, 米;
米;
则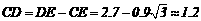 米.
米.
故塑像CD的高大约为1.2米.
19. 证明:
⑴.∵四边形ABCD是正方形 ∴∠ABC=90°,AB=AC, ∵BE⊥BF, ∴∠FBE=90° ∵∠ABE+∠EBA=90° ∠CBF+∠EBA=90° ∴∠ABE=∠CBF 在△AEB和△CFB中
∴△AEB≌△CFB(SAS) ∴AE=CF. | ⑵.∵BE⊥BF, ∴∠FBE=90° 又∵BE=BF, ∴∠BEF=∠EFB=45° ∵四边形ABCD是正方形 ∴∠ABC=90° 又∵∠ABE=55° ∴∠EBG=90﹣55°=35°, ∴∠EGC=∠EBG+∠BEF =45°+35°=80°
|
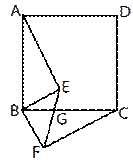
五、解答题(共2个题,每题10分,共20分)
20.解答:
⑴.表中a的值是: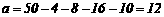
⑵.根据题意画图如下:
⑶.本次测试的优秀率是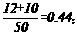
答:本次测试的优秀率是0.44.
⑷.用A表示小宇B表示小强,C、D表示其他两名同学,根据题意画树状图如下:
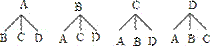
共有12种情况,小宇与小强两名男
同学分在同一组的情况有2种,
则小宇与小强两名男同学分在同一组的概率是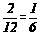 .
.
21.略解:⑴.设王师傅单独整理这批实验器材需要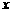 分钟,则王师傅的工作效率为
分钟,则王师傅的工作效率为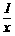 ,
,
由题意,得: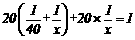 解得:
解得: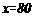 ;经检验得:
;经检验得: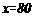 是原方程的根.
是原方程的根.
答:王师傅单独整理这批实验器材需要80分钟.
⑵.设李老师要工作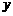 分钟,由题意,得:
分钟,由题意,得: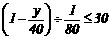 解得:
解得: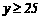
答:李老师至少要工作25分钟.
六、解答题(本题满分12分)
22. 略解:
⑴.分别把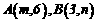 代入
代入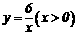 得
得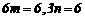 解得
解得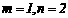 ;
;
所以A点坐标为(1,6),B点坐标为(3,2),分别把A(1,6),B(3,2)
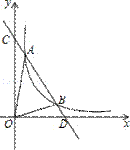 代入
代入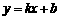 得
得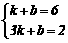 ,解得
,解得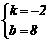 ,所以一次函数解析式为
,所以一次函数解析式为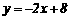 ;
;
⑵.当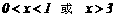 时,
时,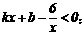
⑶.如图,当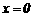 时,
时,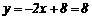 ,则C点坐标为(0,8);
,则C点坐标为(0,8);
当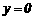 时,
时,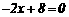 解得:
解得: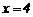 ,则D点坐标为(4,0).
,则D点坐标为(4,0).
所以S△AOB=S△COD﹣S△COA﹣S△BOD=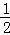 ×4×8﹣
×4×8﹣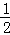 ×8×1﹣
×8×1﹣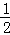 ×4×2==8.
×4×2==8.
七、解答题(本题满分12分)
23.解答:
⑴.∵∠A=∠B=∠DEC=45°,
∴∠AED+∠ADE=135°,∠AED+∠CEB=135°
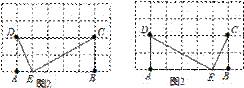 ∴∠ADE=∠CEB,
∴∠ADE=∠CEB,
在△ADE和△BCE中,
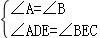 ,
,
∴△ADE∽△BCE,
∴点E是否是四边形ABCD的边AB上的相似点.
⑵.如图所示(图2),点E是四边形ABCD的边AB上的相似点.
⑶.∵点E是四边形ABCM的边AB上的一个强相似点,△AEM∽△BCE∽△ECM.∴∠BC E=∠ECM=∠AEM.由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD.∴
E=∠ECM=∠AEM.由折叠可知:△ECM≌△DCM,∴∠ECM=∠DCM,CE=CD.∴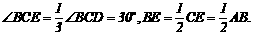 在Rt△BCE中,
在Rt△BCE中,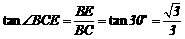 ∴
∴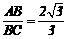 .
.
八、解答题(本题满分14分)
解答:⑴.∵直线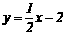 交
交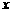 轴、
轴、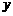 轴
轴 于B、C两点.
于B、C两点.
∴B(4,0),C(0,﹣2).
∵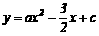 过B、C两点
过B、C两点
∴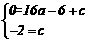 ,解得
,解得 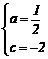 ,∴
,∴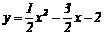 .
.
⑵.证明:如图1,连接AC.

∵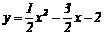 与
与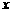 负半轴交于A点,∴A(﹣1,0);在Rt△AOC中,∵AO=1,OC=2,∴
负半轴交于A点,∴A(﹣1,0);在Rt△AOC中,∵AO=1,OC=2,∴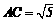
在Rt△BOC中,∵BO=4,OC=2,∴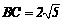 ∵AB=AO+BO=1+4=5, AB2=AC2+BC2,∴△ABC为直角三角形.
∵AB=AO+BO=1+4=5, AB2=AC2+BC2,∴△ABC为直角三角形.
⑶.解:△ABC内部可截出面积最大的矩形DEFG,面积为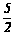 ,理由如下:
,理由如下:

①一点为C,AB、AC、BC边上各有一点,如图2,此时△AGF∽△ACB∽△FEB.
设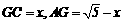 .
. 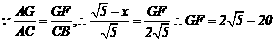
∴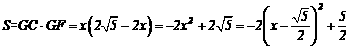 ;即当
;即当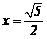 ,S最大,为
,S最大,为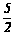 .
.
②AB边上有两点,AC、BC边上各有一点,如图3,此时△CDE∽△CAB∽△GAD,

设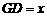 ,则
,则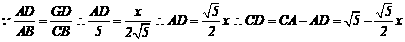
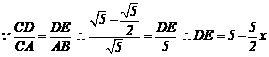
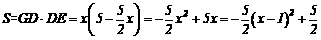 ,
,
即当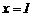 ,S最大,为
,S最大,为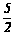 .
.
综上所述,△ABC内 部可截出面积最大的矩形DEFG,面积为
部可截出面积最大的矩形DEFG,面积为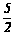 .
.