一、选择题(本大题共12小题,每小题只有唯一正确答案.每小题3分,共36分)
1.若( )×(-2)=1,则括号内填一个实数应该是( )
A.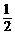 B.2 C.-2 D.-
B.2 C.-2 D.-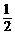
2.下列运算正确的是( )
A.3-1=-3 B.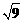 =±3 C.(ab2)3=a3b6 D.a6÷a2=a3
=±3 C.(ab2)3=a3b6 D.a6÷a2=a3
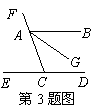
3.如图,AB∥ED,AG平分∠BAC,∠ECF=70°,则∠FAG的度数是( )
A.155° B.145° C.110° D.35°
4.将抛物线y=x2-6x+5向上平移2个单位长度,再向右平移1个单位长度后,得到的抛物线解析式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2 C.y=(x-2)2-2 D.y=(x-1)2-3
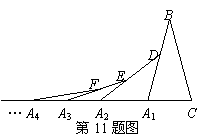
5.已知α是一元二次方程x2-x-1=0较大的根,则下面对α的估计正确的是( )
A.0<α<1 B.1<α<1.5 C.1.5<α<2 D.2<α<3
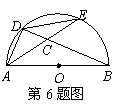
6.如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )
A.∠ACD=∠DAB B.AD=DE C.AD2=BD·CD D.AD·AB=AC·BD




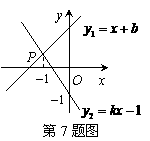
7.如图所示,直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集在数轴上表示正确的是( )

8.如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
A.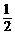 B.
B.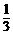 C.
C.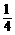 D.
D.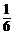
9.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )

A.2种 B.3种 C.4种 D.5种
10.已知:点P(1-2a,a-2)关于原点的对称点在第一象限内,且a为整数,则关于x的分式方程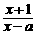 =2的解是( )
=2的解是( )
A.5 B.1 C.3 D.不能确定
11.如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是( )
A.(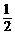 )n·75° B.(
)n·75° B.(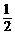 )n-1·65° C.(
)n-1·65° C.(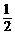 )n-1·75° D.(
)n-1·75° D.(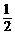 )n·85°
)n·85°
12.如图,已知圆柱底面的周长为4dm,圆柱高为2dm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为( )
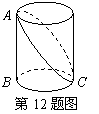
A.4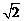 dm B.2
dm B.2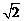 dm C.2
dm C.2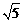 dm D.4
dm D.4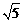 dm
dm
二、填空题(本大题共5小题,每小题3分,共15分)
13.若-2xm-ny2与3x4y2m+n是同类项,则m-3n的立方根是___________.
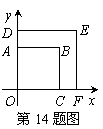
14.如图,正方形OABC与正方形ODEF是位似图形,点O为位似中心,相似比为1∶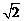 ,点A的坐标为(0,1),则点E的坐标是_________.
,点A的坐标为(0,1),则点E的坐标是_________.
15.我们知道,无限循环小数都可以转化为分数.例如:将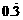 转化为分数时,可设
转化为分数时,可设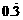 =x,则x=0.3+
=x,则x=0.3+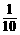 x,解得x=
x,解得x=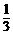 ,即
,即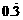 =
=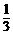 .仿此方法,将
.仿此方法,将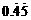 化成分数是_________.
化成分数是_________.
16.如图,在□ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若 的长为
的长为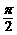 ,则图中阴影部分的面积为_________.
,则图中阴影部分的面积为_________.

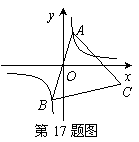
17.如图,已知:点A是双曲线y=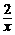 在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=
在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=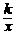 (k>0)上运动,则k的值是_________.
(k>0)上运动,则k的值是_________.
三、解答题(本大题共7题,共69分)
18.(本题满分8分)
(1)计算: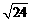 ×
×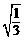 -4×
-4×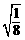 ×(1-
×(1-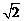 )0;
)0;
(2)先化简,再求值: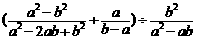 ,其中a,b满足
,其中a,b满足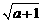 +|b-
+|b- |=0.
|=0.
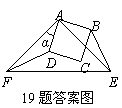
19.(本题满分9分)如图①,正方形ABCD的边AB,AD分别在等腰直角△AEF的腰AE,AF上,点C在△AEF内,则有DF=BE(不必证明).将正方形ABCD绕点A逆时针旋转一定角度α(0°<α<90°)后,连结BE,DF.请在图②中用实线补全图形,这时DF=BE还成立吗?请说明理由.
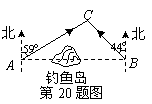
20.(本题满分10分)钓鱼岛自古以来就是中国的领土.如图,我国甲、乙两艘海监执法船某天在钓鱼岛附近海域巡航,某一时刻这两艘船分别位于钓鱼岛正西方向的A处和正东方向的B处,这时两船同时接到立即赶往C处海域巡查的任务,并测得C处位于A处北偏东59°方向、位于B处北偏西44°方向.若甲、乙两船分别沿AC,BC方向航行,其平均速度分别是20海里/小时,18海里/小时,试估算哪艘船先赶到C处.(参考数据:cos59°≈0.52,sin46°≈0.72)
21.(本题满分10分)我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
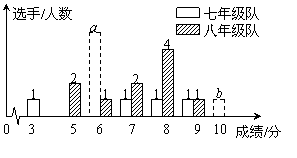

队别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
七年级 | 6.7 | m | 3.41 | 90% | n |
八年级 | 7.1 | 7.5 | 1.69 | 80% | 10% |
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
22.(本题满分10分)我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
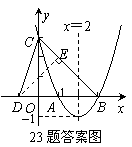
23.(本题满分10分)已知:函数y=ax2-(3a+1)x+2a+1(a为常数).
(1)若该函数图象与坐标轴只有两个交点,求a的值;
(2)若该函数图象是开口向上的抛物线,与x轴相交于点A(x1,0),B(x2,0)两点,与y轴相交于点C,且x2-x1=2.
①求抛物线的解析式;
②作点A关于y轴的对称点D,连结BC,DC,求sin∠DCB的值.
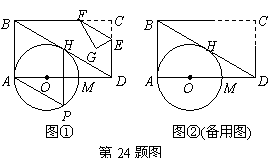
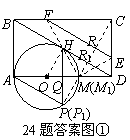
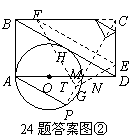
24.(本题满分12分)如图①,已知:在矩形ABCD的边AD上有一点O,OA= ,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
,以O为圆心,OA长为半径作圆,交AD于M,恰好与BD相切于H,过H作弦HP∥AB,弦HP=3.若点E是CD边上一动点(点E与C,D不重合),过E作直线EF∥BD交BC于F,再把△CEF沿着动直线EF对折,点C的对应点为G.设CE=x,△EFG与矩形ABCD重叠部分的面积为S.
(1)求证:四边形ABHP是菱形;
(2)问△EFG的直角顶点G能落在⊙O上吗?若能,求出此时x的值;若不能,请说明理由;
(3)求S与x之间的函数关系式,并直接写出FG与⊙O相切时,S的值.
湖北省荆门市2014年初中毕业生学业水平及升学考试试卷
数学考试答案及评分说明
一、选择题(每小题3分,共36分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | C | B | B | C | D | A | A | C | C | C | A |
7.解:当x>-1时,x+b>kx-1,即不等式x+b>kx-1的解集为x>-1.故选A.
8. 解:
解:
第一个开关
第二个开关
结果:任意闭合其中两个开关的情况共有12种,其中能使小灯泡发光的情况有6种,小灯泡发光的概率是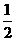 .故选A.
.故选A.
9.解:如图,组成的图形是轴对称图形,又是中心对称图形,这个格点正方形的作法共有4种.故选C.

10.解:根据题意,点P在第三象限内,
∵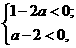 解得
解得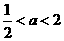 ,∵a为整数,∴a=1.解方程
,∵a为整数,∴a=1.解方程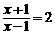 得
得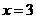 .故选C.
.故选C.
11.解:∵A1B=CB,∠B=30°,∴∠C=∠C A1B=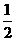 (180°-∠B)=75°.
(180°-∠B)=75°.
又∵A1A2=A1D ,∴∠A1D A2=∠A1 A2D=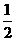 ∠C A1B .
∠C A1B .
 也就是说:自A1以后,这样得来的每一个角都等于前一个角的
也就是说:自A1以后,这样得来的每一个角都等于前一个角的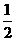 .
.
∴∠An=(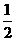 )n-1·75°.故选C.
)n-1·75°.故选C.
12.解:过点A沿直径BC将圆柱纵向切开,得到半圆柱,并将半圆柱,
并将展开为矩形(如图),由题意可知RT△ABC中,AB=BC=2,
∴AC=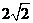 ,∴属丝周长的最小值为2AC=
,∴属丝周长的最小值为2AC=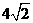 .故选A.
.故选A.
二、填空题(本大题共5小题,每小题3分,共15分)
13.解:∵-2xm-ny2与3x4y2m+n是同类项,∴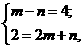 解得
解得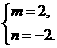
∴m-3n=8. ∴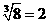 .
.
14.解:根据题意,∵相似比为1∶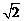 ,∴OA:OD=1∶
,∴OA:OD=1∶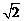 ,
,
∵点A的坐标为(0,1),即OA=1,∴OD=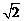 ,
,
∵四边形ODEF是正方形,∴DE= EF=OD=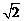 .
.
∴E点的坐标为(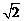 ,
,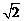 ).
).
15.解:设x=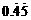 =0.454545……,那么100x=45.4545……,
=0.454545……,那么100x=45.4545……,
而45.4545……=45+0.4545……,
∴100x=45+x化简得99x=45,
解得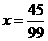 ,
,
∴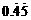 =
=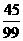 .
.
16.解:连接AC,∵DC是⊙A的切线,∴AC⊥CD.
又∵AB=AC=CD,∴△ACD是等腰直角三角形,∴∠CAD=45°.
又∵四边形ABCD是平行四边形,∴AD∥BC,∴∠CAD=∠ACB=45°.
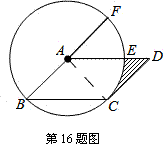 又∵AB=AC,∴∠ACB=∠B=45°,∴∠FAD=45°.
又∵AB=AC,∴∠ACB=∠B=45°,∴∠FAD=45°.
∵ 的长为
的长为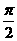 ,∴
,∴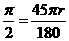 ,解得:
,解得: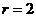 .
.
∴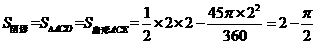 .
.
17.解:设A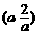 ,∵点A与点B关于原点对称,∴OA=OB.
,∵点A与点B关于原点对称,∴OA=OB.
∵△ABC为等边三角形,∴AB⊥OC,OC=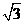 AO,
AO,
∵AO=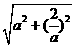 ,∴CO=
,∴CO=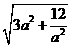 .
.
过点C作CD⊥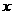 轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),
轴于点D,则可得∠AOD=∠OCD(都是∠COD的余角),
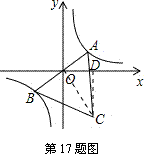 设点C的坐标为
设点C的坐标为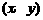 ,则tan∠AOD=tan∠OCD,即
,则tan∠AOD=tan∠OCD,即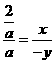 ,解得:
,解得: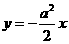 .
.
在Rt△COD中,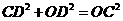 ,即
,即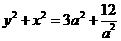 .
.
将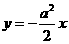 代入,可得:
代入,可得: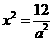 ,故
,故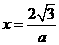 ,
,
∴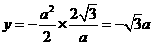 ,则
,则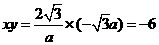 .
.
三、解答题(本题包括7个小题,共69分)
18.解:(1)原式=2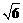 ×
×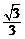 -4×
-4×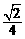 ×1·················· 1分
×1·················· 1分
=2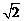 -
-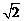 ······························· 2分
······························· 2分
=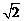 .································· 3分
.································· 3分
(2)原式=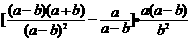
=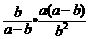 =
=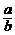 .·························· 5分
.·························· 5分
∵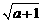 ≥0,|b-
≥0,|b- |≥0,
|≥0,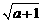 +|b-
+|b- |=0,
|=0,
∴a+1=0且b- =0.∴a=-1,b=
=0.∴a=-1,b= .················ 7分
.················ 7分
∴原式=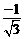 =-
=-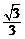 .·························· 8分
.·························· 8分
19.解:补全图形如图所示.························ 3分
DF=BE还成立,理由是:·························· 4分
∵正方形ABCD和等腰△AEF,
∴AD=AB,AF=AE,∠FAE=∠DAB=90°.·················· 6分
∴∠FAD=∠EAB.····························· 7分
在△ADF和△ABE中,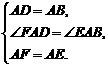
∴△ADF≌△ABE(SAS).∴DF=BE.····················· 9分

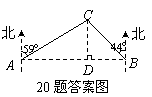

20.解:过C作CD⊥AB于D,设CD=h(海里),两船从A,B到C的时间分别是t甲、t乙(小时),
则∠ACD=59°,∠CBD=90°-44°=46°.
在Rt△ACD中,cos59°=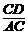 =
=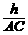 =0.52,则AC=
=0.52,则AC=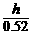 .·········· 3分
.·········· 3分
在Rt△BCD中,sin46°=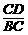 =
=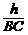 =0.72,则BC=
=0.72,则BC=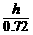 .
.
∴t甲=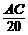 =
=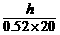 =
=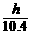 ,t乙=
,t乙=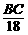 =
=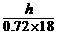 =
=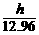 .
.
∵12.96>10.4,
∴t甲>t乙,即乙船先到达C处.······················ 10分
21.解:(1)依题意得: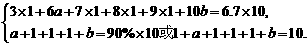 ···· 4分
···· 4分
解得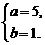 ································ 6分
································ 6分
(2)m=6, n=20%;···························· 8分
(3)①八年级队平均分高于七年级队;②八年级队的成绩比七年级队稳定;③八年级队的成绩集中在中上游,所以支持八年级队成绩好.(注:任说两条即可)····················· 10分
22.解:(1)依题意得:
y=200+50×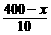 .·························· 2分
.·························· 2分
化简得:y=-5x+2200.························· 3分
(2)依题意有:
∵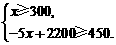 ···························· 5分
···························· 5分
解得300≤x≤350.···························· 6分
(3)由(1)得:w=(-5x+2200)(x-200)
=-5x2+3200x-440000=-5(x-320)2+72000.··············· 8分
∵x=320在300≤x≤350内,∴当x=320时,w最大=72000.
即售价定为320元/台时,可获得最大利润为72000元.············ 10分
23.解:(1)①当a=0时,y=-x+1,有两个交点(0,1),(1,0);······ 1分
②当a≠0且图象过原点时,2a+1=0,a=-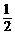 ,有两个交点(0,0),(1,0);·· 2分
,有两个交点(0,0),(1,0);·· 2分
③当a≠0且图象与x轴只有一个交点时,令y=0有:
△=(3a+1)2-4a(2a+1)=0.解得a=-1,有两个交点(0,-1),(1,0);
综上得:a=0或-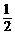 或-1时,函数图象与坐标轴有两个交点.········· 3分
或-1时,函数图象与坐标轴有两个交点.········· 3分
(2)①依题意令y=0时,x1+x2=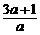 ,x1x2=
,x1x2=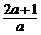 .············ 4分
.············ 4分
由x2-x1=2得:(x2-x1)2=4,则(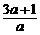 )2-
)2-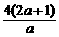 =4.
=4.
化简得:3a2-2a-1=0.解得:a1=-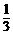 ,a2=1.··············· 5分
,a2=1.··············· 5分
∵△=(3a+1)2-4a(2a+1)=(a+1)2>0,且a>0,
∴a=-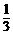 应舍去.a=1符合题意.
应舍去.a=1符合题意.
∴抛物线的解析式为y=x2-4x+3.(注:其它方法,请参照给分) ······· 6分
②令y=0得:x2-4x+3=0.解得:x=1或3.
由x2-x1=2>0知x2>x1,∴A(1,0),B(3,0),D(-1,0),C(0,3).
如图,过D作DE⊥BC于E,则有OB=OC=3,OD=1.
∴DE=BD·sin45°=2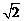 .
.
而CD=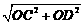 =
=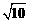 ,
,
∴在Rt△CDE中,sin∠DCB=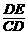 =
=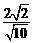 =
=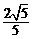 .·············· 10分
.·············· 10分

24.(1)连结OH,如图①.
∵AB∥HP,∠BAD=90°,∴AQ⊥HP.而AM是直径,
∴HQ=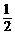 HP=
HP=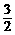 .
.
在Rt△OHQ中,sin∠HOQ=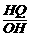 =
=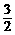 ×
×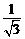 =
=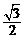 ,
,
∴∠HOQ=60°,则∠OHQ=30°,∠APH=60°.
又BD与⊙O相切,∴∠QHD=90°-∠OHQ=60°.∴∠APH=∠QHD.
∴AP∥BH.
又∵AB∥HP,∴四边形ABHP是平行四边形.················· 3分
由AB⊥AM,AM是直径知AB是⊙O的切线,而BD也是⊙O的切线,
∴AB=BH.
∴四边形ABHP是菱形.(注:其它方法,请参照给分) ············· 4分

(2)G点能落在⊙O上,如图①.
方法一:过C作射线CR⊥EF交EF于R,交AD于M1,交BD于R1,交AP于P1,则C关于EF对称点G在射线CR上.
当G点落在M1上时,M1E=CE=x,AB=CD=HP=3,AD=AB·tan60°=3 ,ED=CD-CE=3-x.
,ED=CD-CE=3-x.
在Rt△M1DE中,cos60°=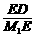 =
=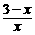 =
=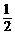 .解得x=2.··········· 6分
.解得x=2.··········· 6分
sin60°=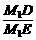 =
=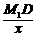 =
=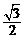 ,∴M1D=
,∴M1D= .
.
而MD=AD-AM= ,∴M1与M重合.···················· 7分
,∴M1与M重合.···················· 7分
∴M在CP1上,则MP1⊥AP,而MP⊥AP,
∴P与P1重合,这校射线CR与⊙O交于M,P.
由AP∥BD,CP⊥AP,CR1=PR1,知C与P关于BD对称.
由于点E不与点D重合,故点G不可能落在P点.
∴点G只能落在⊙O的M点上,此时x=2.·················· 8分
方法二:连结CM,PM,如图①,由(1)知∠AMP=∠APH=60°,tan∠CMD=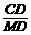 =
=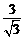 =
= .∴∠CMD=∠AMP=60°.
.∴∠CMD=∠AMP=60°.
∴C,M,P三点共线.
∵∠BDA=30°,∴CM⊥BD.而BD∥EF,
∴CM⊥EF,点C关于EF的对称点G落在CP上.
又∵点P到BD的距离等于点C到BD的距离(即点A到BD的距离),EF与BD不重合,∴点G不能落在P点,可以落在⊙O上的M点.································· 6分
当点G落在⊙O上的M点时,ME=CE=x,
在Rt△MDE中,x=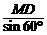 =
= ×
×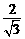 =2.
=2.
∴点G落在床⊙O上的M点,此时x=2.··················· 8分
方法三:证法略.
提示:过C作C′P⊥AP于P′,交BD于R′,可求CP′=2CR′=3 ,PM+CM=3
,PM+CM=3 ,则CP′=CM+MP,从而C,M,P三点共线,x的值求法同上.
,则CP′=CM+MP,从而C,M,P三点共线,x的值求法同上.
(3)由(2)知:①当点G在CM上运动时,0<x≤2,
S=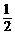 x·
x· x=
x=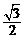 x2.·························· 9分
x2.·························· 9分
②当点G在PM上运动时,2<x<3,设FG交AD于T,EG交AD于N,如图②,

则:EG=CE=x,ED=3-x,S△EFG=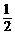 CE·CF=
CE·CF=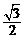 x2.
x2.
NE=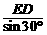 =6-2x,GN=GE-NE=3x-6.
=6-2x,GN=GE-NE=3x-6.
∵TG=GN·tan30°=(3x-6)×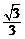 =
= x-2
x-2 .
.
S=S△EFG-S△TGN=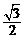 x2-
x2-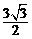 x2+6
x2+6 x-6
x-6
=- x2+6
x2+6 x-6
x-6 .························ 11分
.························ 11分
综上所述,S=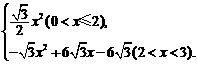
当FG与⊙O相切时,S=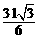 -6.···················· 12分
-6.···················· 12分











